С вихревыми потоками

Согласно представлениям Фарадея магнитные явления обусловлены вихревым движением частиц. То есть магнитные силовые линии образуют в пространстве замкнутые вихревые струйные потоки.

Рассмотрим движение шарового источника, движущегося перпендикулярно силовым линиям струйных потоков, характеризующихся постоянной величиной угловой скорости вращения - .

Решим вначале задачу в плоскости сечения шарового источника перпендикулярной магнитным силовым линиям. В этом случае источник будет представлять собой цилиндр единичной высоты (рис. 1).

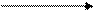
R

В

Направление

движения

источника

Рис. 1

Подставляя в уравнение (3.2.3), указанные на рис. 1 значения, определим проекцию силы, действующую на источник - в направлении , перпендикулярном движению источника:

(3.5.1)

Где:

- орт от центра источника перпендикулярный направлению движения источника;

– орт внешней нормали к поверхности ;

– угол между и ;

– приращение угла ;

- радиус источника;

- скорость частиц, излучаемых источником c поверхности Δs;

- скорость набегающего потока частиц, равная скорости движения источника с

противоположным знаком;

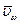- касательная скорость частиц на поверхности ;

- модуль суммарного ускорения частиц, излучаемых источником с поверхности

в направлении , при

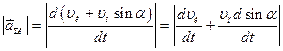(3.5.2)

Перепишем уравнение (3.5.2) с учётом (3.1.7), а также с учётом того, что :

= = (3.5.3)

- модуль суммарного осестремительного ускорения частиц на поверхности

при .

= (3.5.4)

Определим значение: при и при

= (3.5.5)

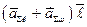= = (3.5.6)

Подставляя найденные значения (3.5.5) и (3.5.6) в (3.5.1), получим:

=

=

=

(3.5.7)

Так как величина действующей силы на единичный цилиндр пропорциональна радиусу цилиндра, то для определения значения силы, действующей в целом на источник ограниченный поверхностью сферы радиуса , достаточно провести интегрирование по всей поверхности сферы:

= = (3.5.8)

Где:

- угол между плоскостью диаметрального сечения сферы, перпендикулярной оси вращения - и направлением от центра сферы к её поверхности;

- радиус сечения сферы плоскостью перпендикулярной , проходящей через точку пересечения сферы лучом, проведенным из центра сферы под углом к её поверхности.

Аналогично определим значение проекции силы, действующей на сток, ограниченный поверхностью сферы радиусом - в направлении , перпендикулярном движению стока:

= (3.5.9)

Подставляя в (2.5.8) и (2.5.9) значения из (2.1.5) и из (2.1.6), получим:

(3.5.10)

(3.5.11)

Дата добавления: 2015-10-13