Электромагнитное взаимодействие двух проводников с током

Согласно представлениям Фарадея и Максвелла, электрический ток при движении вдоль проводника вызывает вихревое движение частиц в окружающем пространстве. Исходя из этих классических представлений, рассмотрим два проводника с током цилиндрической формы длиной . На рис. 1 показано сечение проводников.

проводник I проводник II

.

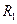
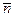
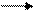
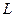
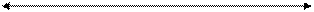
Рис. 1

Где: 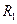и - радиусы сечений проводников I и II соответственно;

и - векторы касательных скоростей вихревого движения частиц на

поверхности проводников I и II соответственно;

- вектор касательной скорости вихревого движения частиц проводника II на

поверхности проводника I;

- вектор суммарной скорости и ;

- плотность частиц в единице объёма;

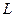- расстояние между центрами проводников;

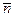- орт внешней нормали к поверхности ;

- орт направления из центра проводника I к центру проводника II;

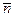- угол между ортами и ;

- приращение угла ;

- элемент поверхности проводника I, образованный пересечением поверхности

проводника I и образующими плоскостями угла .

Радиальными стрелками показано направление вихревого движения частиц проводников I и II – против часовой стрелки.

Тогда, допуская, что касательная скорость вихревого движения частиц убывает обратно пропорционально расстоянию от центра проводников, а также, что расстояние от центра проводника II до элемента поверхности при 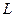>> 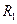стремится к 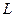, получим:

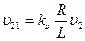(4.3.1)

Где: - коэффициент пропорциональности.

Из рис. 1 определим значение : (4.3.2)

Согласно уравнению Бернулли сила, действующая на элемент поверхности равна: (4.3.3)

Определим элемент цилиндрической поверхности проводника I:

или, переходя к пределу: (4.3.4)

Подставляя в (4.3.3) найденные значения (4.3.2), (4.3.4) и проведя интегрирование по поверхности проводника I в проекции на направление , определим значение силы, действующей на проводник I:

= =

=

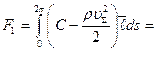
(4.3.5)

Предположим, что скорости частиц 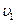и 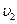пропорциональны величине тока:

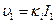(4.3.6)

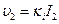(4.3.7)

Где:

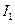- коэффициент пропорциональности;

и - величины тока в проводниках I и II соответственно.

Подставляя в (4.3.5) значения 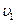(4.3.6), 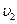(4.3.7), (4.3.1), получим:

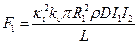(4.3.8)

Аналогично определим значение силы в случае, когда вихревые движения частиц проводников I и II направлены в противоположные стороны:

(4.3.9)

Дата добавления: 2015-10-13