Синтез зубчатых механизмов.

Планетарный механизм с передаточным отношением

Открытая зубчатая передача Z₄ – Z₅ имеет передаточное отношение

U_4-5 =2.406

Синтез (подбор чисел зубьев) планетарной ступени производим на основе следующих четырех условий:

1. Условия выполнения требуемого передаточного отношения:

Откуда: .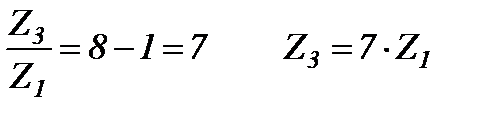

2. Условие правильности зацепления, по которому Z_min ³ 17.

Принимая Z₁ = 18, получаем Z₃ = 7^. 18 = 126

3. Условие соосности

Z₁ + 2Z₂ = Z₃,

откуда Z₂ = 0.5(Z₃ – Z₁) = 0.5(126 – 18) = 54

По условию правильности зацепления:

Z₃ – Z₂ = 126 – 54 = 72 > 8

4. Условие соседства

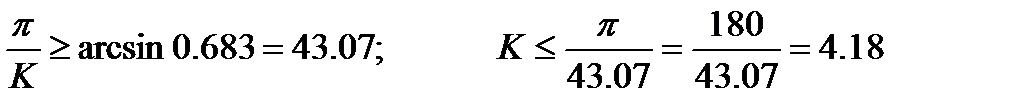
Принимаем число сателлитов К = 4.

Проверяем возможность сборки полученного механизма

,

где К - число сателлитов

П и Ц - целые числа

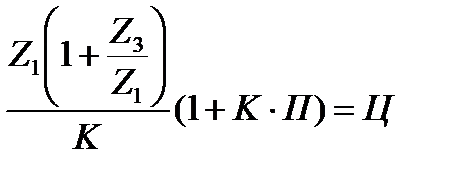
36(1 + КП) = Ц;

Это равенство выполняется при П=0.

Окончательно принимаем для планетарного механизма:

Z₁ = 18; Z₂ = 54; Z₃ = 126; K=4; U_пл = 8.

Для уравнительной зубчатой передачи

Приняв Z₄ = 22, найдем Z₅ = 22 ^. 2.406 = 52

Общее передаточное отношение привода U_пер = 8 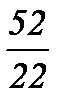^. = 18,909

Расхождение с требуемым % – допускается

Модуль зубчатых колес планетарного редуктора определяем по максимальному моменту в зубчатом механизме, который имеет место на выходном его валу (на валу – водила). Момент на этом валу

где номинальная угловая скорость двигателя

Модуль

Ближайший больший модуль первого ряда по стандарту m = 5,0 мм.

Модуль зубчатых колес уравнительной передачи рассчитываем по моменту на валу кривошипа

Тогда

Принимаем m₁ = 6 мм.

Определяем делительные диаметры колес: d_i = m_i ^. Z_i

d₁=5^.18= 90 мм.

d₂=5 ^. 54=270 мм.

d₃=5 ^. 126=630 мм.

d₄=6 ^, 22=132 мм.

d₅=6 ^. 52=312 мм

и диаметр водила Н

d_H > d₁ + 2d₂ / 2 = 90 + 270 = 360 мм.

Дата добавления: 2015-10-13