Определение скоростей и ускорений.

Чтобы воспользоваться принципом Даламбера, необходимо найти ускорения центров масс и угловые ускорения звеньев. Эту задачу решаем путем построения плана ускорений.

В расчетном, 3-ем положении, рассматриваемой кинематической цепи при установившемся режиме движения из табл.3.1. находим:

w₁ = 7.914 с^-1

а с помощью графика w₁ = f (j₁₀) определяем:

Знак " – " указывает на то, что e₁ и w₁ направлены противоположно.

Для определения сил инерции звеньев шестизвенника АВСDЕ строим для него план ускорений, начиная от входного звена АВ.

По теореме о вращательном движении кривошипа АВ, ускорение точки В:

где нормальная составляющая ускорения

7.914^{2 .} 0.109 = 6.83 м./с²

в масштабе построения

m_а =0,05 м/с²мм

на чертеже отложена в векторе с модулем pn₁ =136,6 мм в направлении от точки В кривошипа АВ к центру его вращения А, а тангенциальная составляющая

1.492 ^. 0.109 = 0.163 м/с²

отложена в векторе с модулем n₁a =3,26 мм в соответствии с направлением углового ускорения e₁ перпендикулярно вектору

По теореме о плоском движении точки С в системе шатуна ВС и движении этой точки в системе коромысла СD имеем векторное равенство

Чтобы решить это уравнение, определяем нормальные составляющие ускорений

где

Из таблицы 2.6. выписываем значения передаточных функций

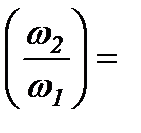0.023 0.275

находим при w₁ = 7.914 с^-1

w₂ = 7.914 ^. 0.023 = 0.182 с^-1

w₃ = 7.914 ^. 0.275 = 2.176 с^-1

0.182^2. 0.306 = 0.010 м/с²

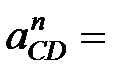2.176^2. 0.38 = 1.8 м/с²

Отрезки, изображающие эти ускорения в масштабе плана ускорений, имеют величину

После графического решения уравнения имеем: pc = dс =143.5 мм

n₂c= 219,7 мм

n₃c = 139.0 мм

bc = 219,7 мм

Находим положение точек E и S₂ (CS₂ = BS₂)

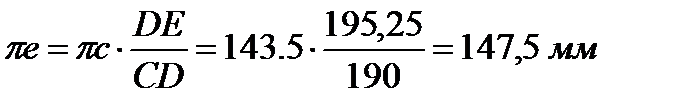
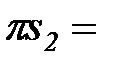87 мм (замеряем на чертеже)

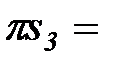0

Ускорения центров масс и угловые ускорения звеньев

87.0 ^. 0.05 = 4.35 м/с²

0

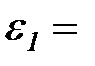1.492 с^-2

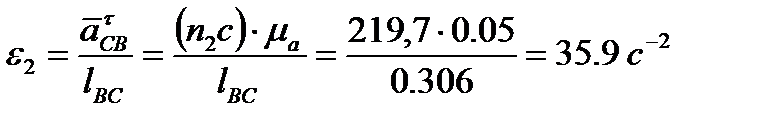
По теореме о плоском движении точки E в системе ползунов 4 и 5 имеем векторное равенство

где - параллельно линии движения звена 5;

параллельно линии относительного движения звена 4 (параллельно DE).

ускорение Кориолиса направление ускорения Кориолиса определяется поворотом вектора относительной скорости (вектор на плане скоростей) на 90° в направлении угловой скорости звена 3.

Из таблицы 2.6. выписываем значение передаточной функции для расчетного положения 4.

На чертеже

После графического решения уравнения с чертежа имеем

133,3 мм

a_S5 = pе₅^. m_a = 133,3 ^. 0.05 = 6,665 м/с²

Дата добавления: 2015-10-13