
Читайте также:
|
Инертные свойства машин и механизмов характеризуют приведенной массой, либо приведенным моментом инерции, в зависимости от того, линейным или угловым является перемещение звена приведения.
Приведенный к звену момент инерции масс звеньев механизма вычисляют как сумму произведений масс этих звеньев и их моментов инерции на квадраты передаточных функций в движениях звеньев относительно звена приведения.
Приведенный момент инерции механизма может быть приведен к главному валу машины, для чего его величину умножают на квадрат передаточной функции от звена приведения к указанному валу.
Приведенный к главному валу машины момент инерции ее маховых масс вычисляют как сумму произведений масс и моментов инерции ее звеньев, а также приведенных масс: либо приведенных моментов инерции ее механизмов, на квадраты передаточных функций в движении приводимых звеньев и звеньев приведения относительно вала машины, принятого за главный.
Т.о., приведенный к валу кривошипа АВ принимаемый за главный момент инерции масс насоса, может быть представлен в виде суммы приведения моментов инерции следующих четырех механизмов насоса:
1. Ротора приводного электродвигателя
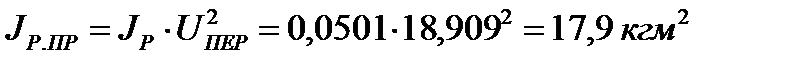
2. Зубчатой передачи
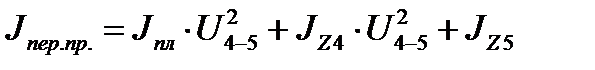
где 
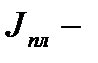 приведенный к валу водила Н момент инерции планетарного механизма зубчатой передачи.
приведенный к валу водила Н момент инерции планетарного механизма зубчатой передачи.
Величину 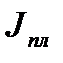 вычисляем, пользуясь
вычисляем, пользуясь
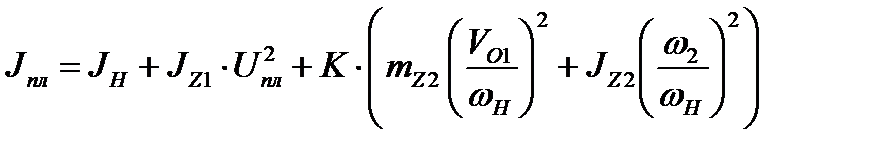
где 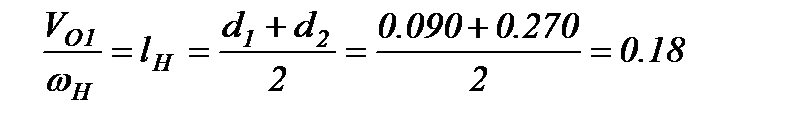
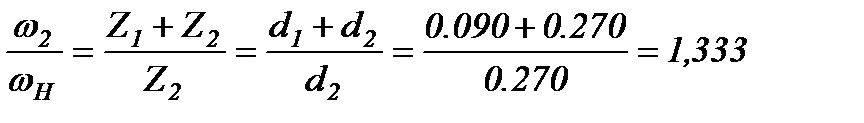
Таким образом Jпл = 0.578 + 0.00226 .82 +4(20.1 . 0.182 + 0.183 . 1.3332)=4.628 кгм2
Jпер.пр = (4.628 +0,0129) .2,36362 + 0.402 = 26.33 кгм2
3. Приведенного к валу кривошипа момента инерции кулачкового механизма. Указанный момент влияет на движение насоса лишь в периоды движения толкателя кулачкового механизма – на фазах удаления и возвращения. Причем, на концах этих фаз 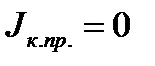 т.к. передаточная функция
т.к. передаточная функция  от толкателя к кулачку. т. е. к валу кривошипа АВ, при этом равна 0.
от толкателя к кулачку. т. е. к валу кривошипа АВ, при этом равна 0.
Максимальное значение 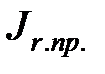 приобретает вблизи середины этих фаз, когда
приобретает вблизи середины этих фаз, когда 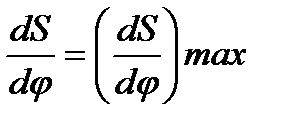
Положение 2 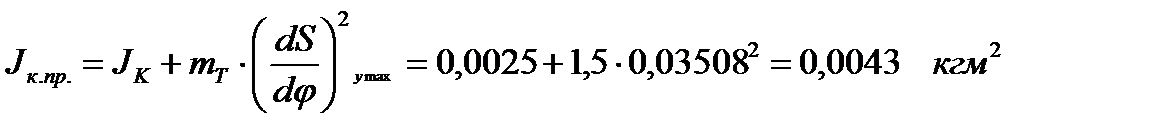
Положение 4 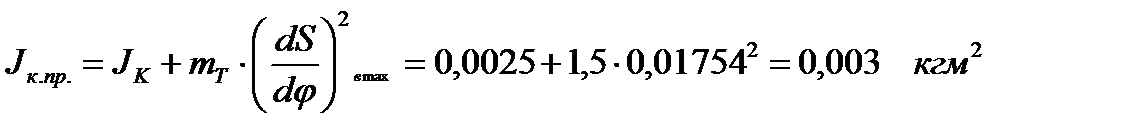
Во всех остальных положениях 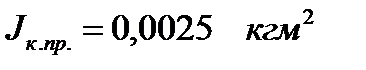
4. Приведенного к валу входного кривошипа АВ момента инерции несущего механизма (рис. 2.7.)
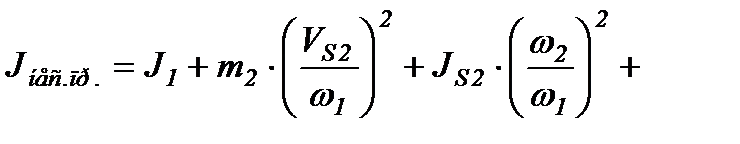
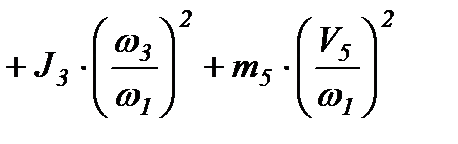
Ранее получены размеры звеньев, массы и моменты инерции:
lAВ = 0.109 м lOS1 = 0 m1 = 0 кг
J1 = 0 кгм2
lBС = 0.306 м lВS2 = 0.153 м m2 = 9,2 кг
JS2 = 0.072 кгм2
l3’ = 0.38 м
l3’’ = 0.44 м lDS3 = 0 m3 = 24.6 кг
J3 = 1.402 кгм2
m5 = 7,4 кг
lАD = 0.38 м h = 0.3847 м
В соответствии с ([3], стр. 82-85 и [5], стр. 161-162) для шарнирного четырехзвенника АВСD имеем:

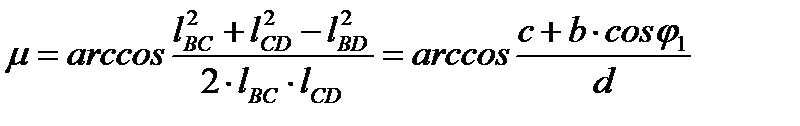
где 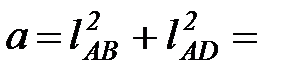 0.1092 + 0.382 = 0.1563 м2
0.1092 + 0.382 = 0.1563 м2
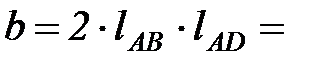 2 . 0.109 . 0.38 = 0.0828 м2
2 . 0.109 . 0.38 = 0.0828 м2
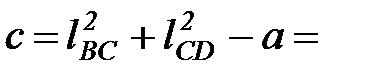 0.3062 + 0.382 – 0,1563 = 0.0818 м2
0.3062 + 0.382 – 0,1563 = 0.0818 м2
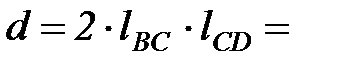 2 . 0.306 . 0.38 = 0.2326 м2
2 . 0.306 . 0.38 = 0.2326 м2
Далее получаем: 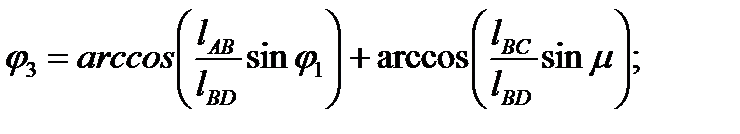


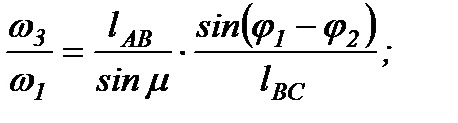
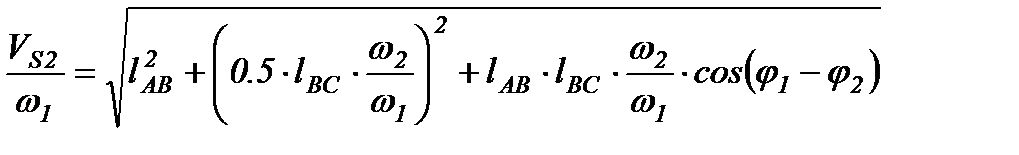
Для присоединенного тангенсного механизма СDE ([3], стр. 82-85 и [5], стр. 161-162)
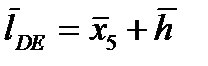
в проекциях на оси координат 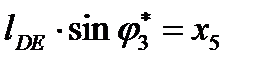
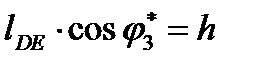
где из рис.2.7. 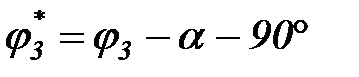 , а
, а 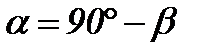
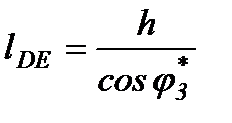
Передаточные функции 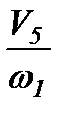 и
и 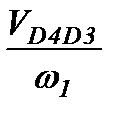 вычисляем дифференцируя уравнения проекций
вычисляем дифференцируя уравнения проекций
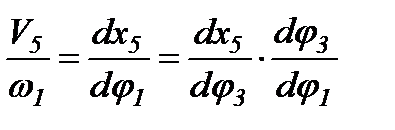
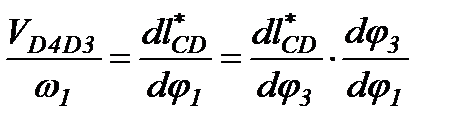
где 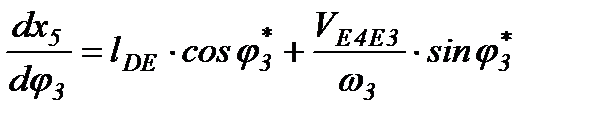
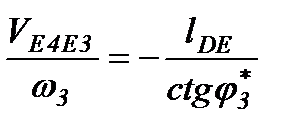
Расчеты передаточных функций сводим в таблицу 6.
Таблица 6
| № пол. | j1 град. | m град. | j2 град. | j3 град. | S5 м. | w2/w1 |
| 255,00 | 75,0 | 75,0 | 150,0 | 0,0000 | 0,356 | |
| 270,00 | 69,4 | 80,1 | 149,6 | 0,0029 | 0,328 | |
| 294,50 | 60,0 | 87,1 | 147,1 | 0,0210 | 0,221 | |
| 319,00 | 51,7 | 90,2 | 141,9 | 0,0596 | 0,023 | |
| 8,00 | 45,2 | 78,7 | 123,9 | 0,1790 | -0,451 | |
| 57,00 | 56,9 | 56,9 | 113,8 | 0,2500 | -0,356 | |
| 72,00 | 62,5 | 52,2 | 114,7 | 0,2443 | -0,272 | |
| 133,00 | 83,8 | 45,0 | 128,8 | 0,1500 | 0,026 | |
| 194,00 | 89,7 | 53,7 | 143,4 | 0,0472 | 0,275 | |
| 255,00 | 75,0 | 75,0 | 150,0 | 0,0000 | 0,356 |
| № пол. | w3/w1 | VS2/w1 м. | VS3/w1 м. | V5/w1 м. | VE4E3/w1 м. |
| 0,000 | 0,055 | 0,000 | 0,000 | 0,000 | |
| -0,052 | 0,060 | 0,000 | -0,022 | 0,007 | |
| -0,153 | 0,080 | 0,000 | -0,063 | 0,016 | |
| -0,275 | 0,107 | 0,000 | -0,109 | 0,019 | |
| -0,381 | 0,108 | 0,000 | -0,150 | -0,021 | |
| 0,000 | 0,055 | 0,000 | 0,000 | 0,000 | |
| 0,110 | 0,071 | 0,000 | 0,046 | 0,014 | |
| 0,288 | 0,109 | 0,000 | 0,111 | 0,006 | |
| 0,183 | 0,081 | 0,000 | 0,073 | -0,014 | |
| 0,000 | 0,055 | 0,000 | 0,000 | 0,000 |
Результатами таблицы 6 пользуемся для определения моментов инерции масс подвижных звеньев несущего механизма насоса. В таблицу 7, помещаем также сведения об изменении моментов инерции масс звеньев прочих механизмов насоса- зубчатой передачи, кулачкового механизма, ротора приводного электродвигателя, сведения об изменении работ сил, приращениях кинематической энергии.
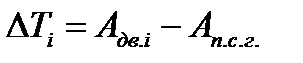
Табл.7.
| №№ пол. | Обобщ. коорд. j10 град. | Работа сил | Приращ.
кинетич.
энергии
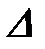 Т кDж. Т кDж.
| Момент инерции, приведенный к валу кривошипа АВ кгм2 | |||||
| А д кDж. | Ас кDж. | Jр.пр | Jпер.пр | Jк.пр. | Jнес.пр. | 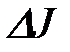
| |||
| 0,0 | 0,000 | 0,000 | 0,000 | 17,90 | 26,33 | 0,0025 | 0,0365 | 0,0390 | |
| 15,0 | 0,514 | 0,072 | 0,442 | 17,90 | 26,33 | 0,0025 | 0,0498 | 0,0523 | |
| 39,5 | 1,353 | 0,868 | 0,485 | 17,90 | 26,33 | 0,0043 | 0,1354 | 0,1397 | |
| 64,0 | 2,192 | 2,564 | -0,372 | 17,90 | 26,33 | 0,0025 | 0,3297 | 0,3322 | |
| 113,0 | 3,870 | 7,815 | -3,945 | 17,90 | 26,33 | 0,0030 | 0,5500 | 0,5530 | |
| 162,0 | 5,549 | 10,941 | -5,393 | 17,90 | 26,33 | 0,0025 | 0,0365 | 0,0390 | |
| 177,0 | 6,062 | 10,796 | -4,734 | 17,90 | 26,33 | 0,0025 | 0,0904 | 0,0929 | |
| 238,0 | 8,152 | 11,388 | -3,237 | 17,90 | 26,33 | 0,0025 | 0,3502 | 0,3527 | |
| 299,0 | 10,241 | 12,034 | -1,793 | 17,90 | 26,33 | 0,0025 | 0,1671 | 0,1696 | |
| 360,0 | 12,330 | 12,330 | 0,000 | 17,90 | 26,33 | 0,0025 | 0,0365 | 0,0390 |
График работ 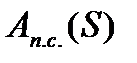 и
и 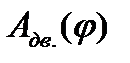 получены путем интегрирования графиков полезных и движущих сил
получены путем интегрирования графиков полезных и движущих сил 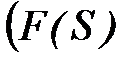 и
и 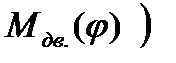 в пределах одного полного цикла установившегося движения насоса в предположении, что при допускаемых изменениях угловой скорости главного вала внутри цикла установившегося движения момент приводного асинхронного электродвигателя будет практически постоянным, а работы полезных и движущих сил в конце цикла окажутся одинаковыми.
в пределах одного полного цикла установившегося движения насоса в предположении, что при допускаемых изменениях угловой скорости главного вала внутри цикла установившегося движения момент приводного асинхронного электродвигателя будет практически постоянным, а работы полезных и движущих сил в конце цикла окажутся одинаковыми.

Полученная при этом пропорциональная зависимость 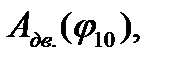 где
где 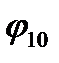 - обобщенная координата, замеренная от начального (нулевого) положения кривошипа (соответствует началу рабочего хода поршня) позволяет вычислить текущие значения работ движущихся сил
- обобщенная координата, замеренная от начального (нулевого) положения кривошипа (соответствует началу рабочего хода поршня) позволяет вычислить текущие значения работ движущихся сил  как
как 
где в свою очередь 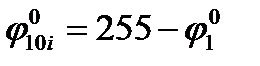
Результатами таблицы 7 в дальнейшем воспользуемся для решения задачи об определении маховых масс насоса, которыми необходимо дополнить уже имеющиеся массы механизмов, чтобы технологический процесс был динамически устойчивым и протекал в нужном ритме.
Необходимость в дополнительной маховой массе может быть установлена с помощью диаграммы энергомасс с учетом коэффициента неравномерности хода главного вала  , который будет соответствовать для насосов
, который будет соответствовать для насосов 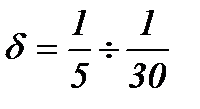 ([2], табл. 5, стр. 376). Принимаем
([2], табл. 5, стр. 376). Принимаем  .
.
Задачу построения указанной диаграммы решаем в два этапа: в начале в соответствующих осях устанавливаем ее общий вид, затем находим оси, в которых эта диаграмма соответствует рекомендуемой величине коэффициента 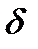 .
.
Известно, что вид графика определяют либо абсолютными координатами точек, либо приращениями этих координат. Поэтому текущие значения кинетической энергии масс звеньев насоса и приведенных моментов инерции этих масс представим в виде сумм искомых констант и известных их приращений:
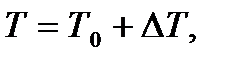

где 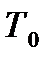 - неизвестный запас кинетической энергии насоса обеспечивающий динамическую устойчивость его работы,
- неизвестный запас кинетической энергии насоса обеспечивающий динамическую устойчивость его работы, 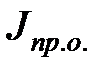 - приведенный момент инерции масс насоса отнесенный к неизменяемой его части(механизмы с неизменяемой геометрией, например, зубчатые механизмы, отдельные звенья, ротор электродвигателя и т.п.).
- приведенный момент инерции масс насоса отнесенный к неизменяемой его части(механизмы с неизменяемой геометрией, например, зубчатые механизмы, отдельные звенья, ротор электродвигателя и т.п.).
В нашем случае:
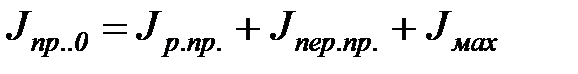
где 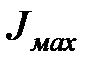 -приведенный момент инерции искомой дополнительной маховой массы махового колеса, который, возможно придется ввести для повышения равномерности вращения кривошипа АВ и, следовательно, ротора электродвигателя.
-приведенный момент инерции искомой дополнительной маховой массы махового колеса, который, возможно придется ввести для повышения равномерности вращения кривошипа АВ и, следовательно, ротора электродвигателя.
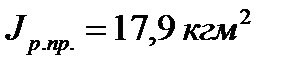 ;
; 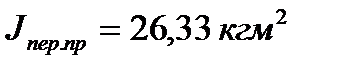 - известные составляющие постоянной части приведенного момента инерции (табл.7.)
- известные составляющие постоянной части приведенного момента инерции (табл.7.)
Известные приращения:

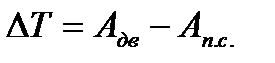
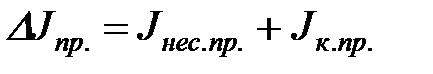
В осях приращений 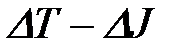 (лист1) в масштабах по осям
(лист1) в масштабах по осям
энергии 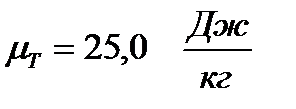
и приведенного момента инерции 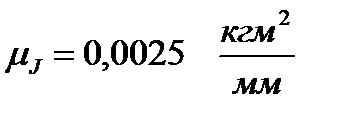
строим диаграмму энергомасс за цикл установившегося движения. Чтобы найти оси этой диаграммы 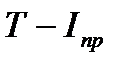 вычисляем углы наклона касательных к ней
вычисляем углы наклона касательных к ней 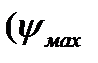 и
и 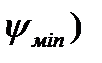 которые должны пересекаться в начале координат
которые должны пересекаться в начале координат 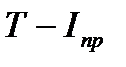
Имеем: 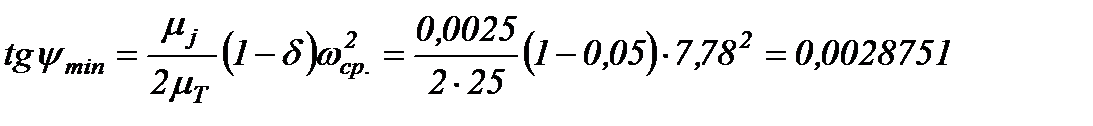
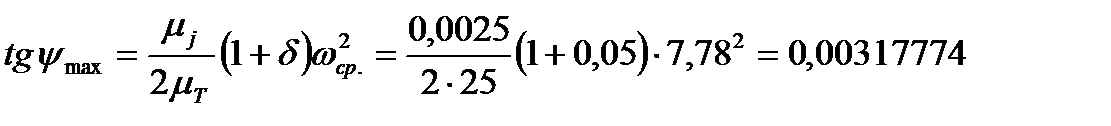
где средняя угловая скорость главного вала насоса
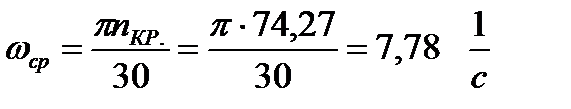
Проводя касательные под найденными углами 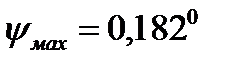 и
и 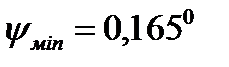 , к диаграмме, получаем точку пересечения касательных О, а также константы
, к диаграмме, получаем точку пересечения касательных О, а также константы 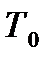 и
и 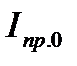
Положение точки 0 в нашем случае выходит за пределы чертежа. Поэтому задачу об определении названных констант решаем аналитически.
Записываем уравнение касательных как прямых, отсекающих на оси 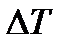 отрезки
отрезки 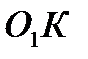 и
и 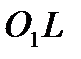 проходящих в известных направлениях (под углами
проходящих в известных направлениях (под углами 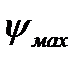 и
и 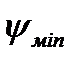 )
)
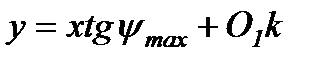
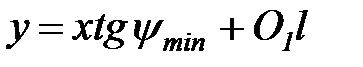
Отрезки 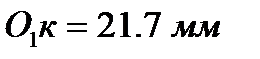 ,
, 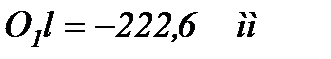
Решая эти уравнения совместно, получаем координаты их общей точки (точки О) в осях 
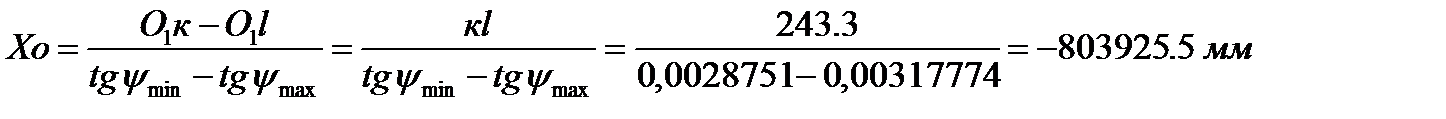
При этом из первого уравнения
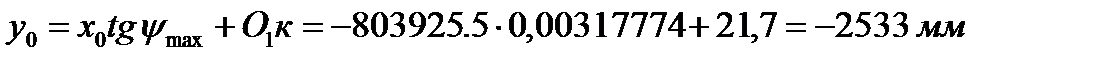
Следовательно
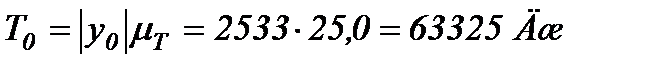
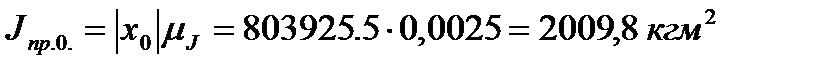
Момент инерции махового колеса, которое необходимо закрепить на главном валу насоса (вал кривошипа АВ) должен составлять
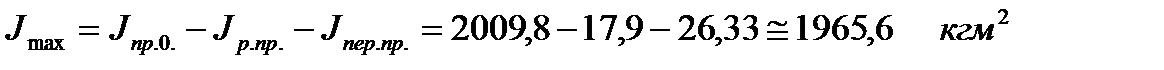
При диаметре маховика 1 м масса маховика (сплошного диска)
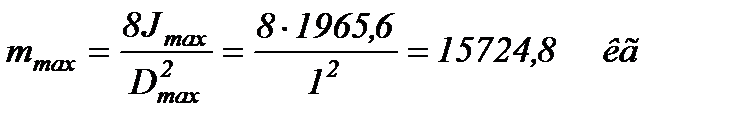
Такой маховик будет запасать кинетическую энергию
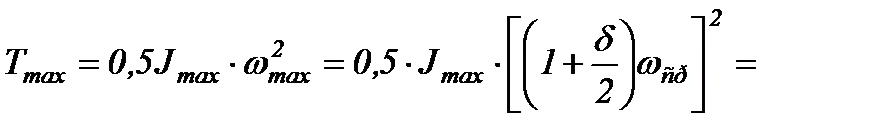
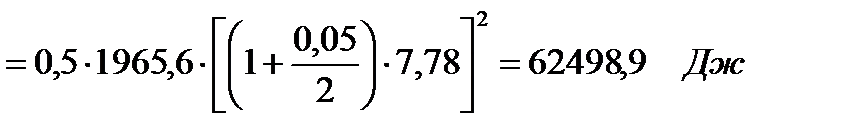
Эту уже энергию маховик может запасти на любом валу насоса, в том числе на валу приводного электродвигателя, который по сравнению с валом кривошипа АВ является более быстроходным. При размещении маховика на валу приводного электродвигателя его момент инерции может быть существенно уменьшен:
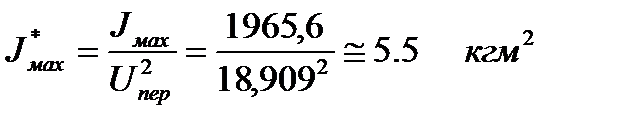
при этом масса составляет:
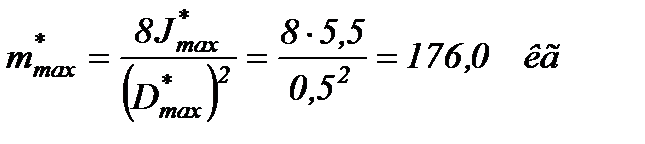
где 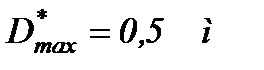 - принятый диаметр маховика.
- принятый диаметр маховика.
Дата добавления: 2015-10-13; просмотров: 280 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Расчет массы и моментов инерции звеньев | | | Определение расхода материалов и энергии при запуске насоса. |