Решение. Построим область допустимых решений D (рис

Построим область допустимых решений D (рис. 1.3).

Построение области аналогично примеру 2, но в этом построении отсутствует прямая y ₄.

Пересечение трех полуплоскостей с учетом естественных ограничений определяет неограниченную область допустимых решений D.

Рис. 1.3

Построим вектор-градиент из начала координат. Проведем линию перпендикулярно вектору– 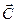. Линия F 1, проходящая через начало координат, соответствует значению 1, поскольку .

Мысленно сдвинем линию уровня в направлении вектора 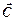. Первое касание многоугольника соответствует положению F 3. Эта линия является опорной, и ей соответствует минимальное значение, которое достигается на множестве допустимых решений. Заметим, что многогранник незамкнут в направлении роста целевой функции, поэтому целевая функция не имеет максимума. Это объясняется тем, что для любой линии уровня найдется другая линия уровня, лежащая в направлении вектора 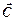, которой соответствует большее значение функции.

Вывод. Целевая функция не ограничена, если многогранник незамкнут в направлении роста целевой функции.

Дата добавления: 2015-09-03