Тема 1 . Задачи математического программирования

Цель работы:

· изучить основные понятия линейного программирования;

· освоить графический метод решения простейших задач линейного программирования;

· научиться использовать сим­плексный метод с искусственным базисом на примере задачи о диете.

1. Основная задача линейного программирования

1.1. Основные формулы и определения

В каноническом виде задача линейного программирования (ЛП) формулируется следующим образом.

Найти такой набор , который является решением системы

(1.1)

удовлетворяет соотношению

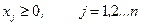
(1.2)

и обеспечивает максимум (минимум) линейной функции

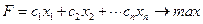
(1.3)

Соотношения (1.1) принято называть фазовыми ограничениями, соотношения (1.2) – естественными ограничениями.

Функцию F принято называть целевой функцией.

Система ограничений всегда может быть приведена к каноническому виду.

Если ограничения заданы неравенствами, то их можно преобразовать в равенства путем введения новых неотрицательных переменных, так называемых балансовых (выравнивающих) ресурсов.

Так, например, в неравенстве достаточно добавить к левой части некоторую величину x_n+1³0 и получится равенство: .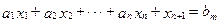

Чтобы балансовые переменные не влияли на искомый оптимум, их вводят в целевую функцию (1.1) с нулевыми коэффициентами.

В дальнейшем будет рассматриваться только задача на максимизацию. Если необходимо решить задачу на минимизацию линейной формы, то коэффициенты целевой функции следует умножить на (-1) и решать эту новую задачу на максимум. Искомый минимум целевой функции получается умножением найденного максимального значения на (-1), т.е. .

Задачу ЛП, определяемую соотношениями (1.1)-(1.3), можно записать в матричном виде:

,

,

,

где , , ,

.

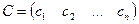В дальнейшем при анализе задачи также используется расширенная матрица системы (1.1) , которая составляется из матрицы А и вектора В.

Дата добавления: 2015-09-03