Пример 1. Задача о диете.

Составить задачу ЛП, позволяющую оптимизировать расход кормов, и привести ее к каноническому виду.

Для откорма животных употребляют два вида кормов; стоимость 1 кг корма I вида - 5 у.е., а корма - II вида 2 у.е. В каждом килограмме корма I вида содержится 5 ед. питательного вещества А, 2.5 ед. питательного вещества B и 1 ед. питательного вещества C. В каждом килограмме корма II вида содержится соответственно 3, 3 и 1.3 ед. Суточный рацион предусматривает питательных единиц A не менее 225 ед., типа B - не менее 150 ед. и типа C - не менее 80 ед. Какое количество корма каждого вида необходимо расходовать ежедневно, чтобы затраты были минимальны?

Решение

Построим математическую модель данной задачи. Обозначим через x ₁ и x ₂ количество кормов I и II вида соответственно. Тогда суммарная стоимость кормов будет равна 5 x ₁ +2 x ₂. Поэтому целевая функция будет иметь вид:

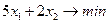
(1.4)

Ограничения по содержанию питательных веществ в рационе будут иметь вид:

	(1.5)
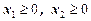
	(1.6)

Соотношения (1.4)-(1.6) корректно определяют задачу ЛП, но предложенная форма записи не является канонической. Для приведения задачи к этой форме домножим ЦФ (1.4) на –1, в результате получим новую ЦФ (1.7). Для преобразования фазовых ограничений (1.5) к канонической форме введем положительные балансовые переменные x ₃, x ₄ и x ₅. Тогда фазовые ограничения примут вид (1.8), а естественные - вид (1.9).

(1.7)

	(1.8)
	(1.9)

Соотношения (1.7) – (1.9) определяют задачу ЛП в канонической форме.

1.2. Симплекс-метод

1.2.1. Геометрическая интерпретация

Геометрическое истолкование симплекс-метода наиболее просто может быть проиллюстрировано в случае двух переменных.

Положение 1.

Каждое неравенство 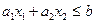с двумя переменными x ₁ и x ₂ определяет полуплоскость в системе координат x ₁ 0 x ₂.

Положение 2.

В случае, когда задана система неравенств

(1.10)

то она определяет многоугольную область D на плоскости, которая является результатом пересечения m полуплоскостей. Область D называется областью решений системы неравенств. Область D может быть ограниченной, неограниченной или пустой. Область решений D обладает важным свойством – она является выпуклой.

Определение 1. Область называется выпуклой, если она вместе с любыми двумя точками содержит весь отрезок их соединяющий.

Определение 2. Прямая называется опорной по отношению к области, если:

1) имеет с областью по крайней мере одну общую точку;

2) вся область лежит по одну сторону от этой прямой.

Положение 3. Пусть задана линейная функция

(1.11)

Для каждой точки плоскости в системе координат x ₁ 0 x ₂. функция F принимает фиксированное значение F=F ₁.

Определение 3. Множество точек, в которых функция двух переменных принимает фиксированное значение, называется линией уровня.

Линия уровня для линейной функции – прямая, которая определяется уравнением . Придавая F ₁ различные значения, получим различные линии уровня.

Все линии уровня (для линейной функции) параллельны между собой.

Нормаль к линии уровня определяется через градиент функции. Градиент произвольной функции двух переменных f (x _1, x ₂) может быть вычислен по формуле

,

(1.12)

поэтому градиент линейной функции определяется уравнением , т.е. градиент может быть задан вектором , выходящим из начала координат.

Градиент указывает направление наибыстрейшего роста функции в данной точке.

Положение 4. Графическое решение задачи ЛП, определяемой фазовыми ограничениями (1.10), естественными ограничениями и целевой функцией (1.11), основано на мысленном эксперименте по перемещению линии уровня относительно области допустимых решений D. Область допустимых решений D задачи ЛП – это множество точек, координаты которых удовлетворяют фазовым и естественным ограничениям. Допустим, множество D ограничено. Пусть при движении прямой F ₁ в положительном направлении вектора 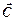она впервые встретится с многоугольником решений в его вершине, тогда в этом положении прямая F ₁ становится опорной, и на этой прямой функция F принимает наименьшее значение. При дальнейшем движении в том же направлении прямая F ₁ пройдет через другую вершину многоугольника решений (выходя из области решений), и станет также опорной прямой; на ней функция F принимает наибольшее значение среди всех значений, принимаемых на многоугольнике решений.

Таким образом, максимизация линейной функции на многоугольнике решений достигается в точке пересечения этого многоугольника с опорными прямыми, перпендикулярными вектору .

Положение 5. Существование решения и количество решений задачи ЛП основано на анализе взаимного расположения области допустимых решений D и линии уровня.

Если область D ограничена, то возможны два варианта:

А) опорная прямая имеет с многоугольником одну общую точку – одно решение;

Б) опорная прямая параллельна стороне многоугольника (на которой достигается максимум) – множество решений (вся сторона многоугольника).

Если область D не ограничена, то возможны три варианта:

А) опорная прямая имеет с многоугольником одну общую точку – одно решение;

Б) опорная прямая параллельна стороне многоугольника (на которой достигается максимум) – имеется множество решений;

В) не существует опорной прямой (в направлении роста функции) - множество решений пусто (нет решений).

Дата добавления: 2015-09-03