
Читайте также:
|
Составим математическую модель для данной задачи. Пусть x j – количество выпускаемой продукции j -го типа, j=1,2,3,4. Как видно из таблицы 2.1, для выпуска одного квадратного метра блочного жилья требуется 1 единица электроэнергии, значит, для выпуска всего количества блочного жилья потребуется 1 x j единиц электроэнергии, для строительства всего количества панельного жилья потребуется 3 x 2 единиц электроэнергии и т.д. Таким образом, ограничение по электроэнергии будет иметь вид: 1 x 1+3 x 2+2 x 3+1 x 4£100. В этом ограничении левая часть показывает потребность в ресурсе (затраты электроэнергии на строительство жилья в объемах x 1, x 2, x 3, x 4), а правая – его имеющееся количество в наличии.
Аналогично можно составить ограничения для других ресурсов и написать зависимость для целевой функции. Тогда математическая модель задачи будет иметь следующий вид:

| (2.7) |

| (2.8) |

| (2.9) |
Задача может быть решена симплекс-методом, описанным выше. Сами симплекс-таблицы могут быть могут быть оформлены с использованием MS Excel. Возможный вариант оформления приведен на рис. 2.3. Решением задачи (2.7)-(2.9) является набор
x1 =20, x2 =0, x3 =0, x4 =20,
а значение целевой функции равно 290. Это означает, что выгодно производить продукцию первого и четвертого вида в количестве 20 единиц каждого, производить продукцию второго и третьего вида не выгодно. Суммарная величина прибыли при этом равна 290.
Заметим, что целевая функция после последней итерации будет иметь вид:

| (2.10) |
Коэффициенты 2 и 4, взятые с противоположным знаком, при  и
и  являются нормированной стоимостью продукции второго и третьего видов. Коэффициенты 4.5 и 0.1, взятые с противоположным знаком, при
являются нормированной стоимостью продукции второго и третьего видов. Коэффициенты 4.5 и 0.1, взятые с противоположным знаком, при  и
и 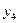 являются теневой ценой ресурсов второго и четвертого видов.
являются теневой ценой ресурсов второго и четвертого видов.

Рис.2.3. Решение в MS Excel симплекс-методом
Рассмотрим решение задачи в MS Excel c помощью надстройки Поиск решения.
1. Разместим на рабочем листе MS Excel исходные данные, как показано на рис.2.4: в ячейках B3:E3 значения переменных можно положить равными 0, в ячейке F4 значение целевой функции вычисляется по формуле =СУММПРОИЗВ(B3:E3;B4:E4). Левая часть ограничений вычисляется следующим образом: в ячейку F7 заносится формула =СУММПРОИЗВ($B$3:$E$3;B7:E7), после чего она копируется в ячейки F8:F11.
Примечание: встроенная функция СУММПРОИЗВ(U,V), где U и V - интервалы ячеек, имеющих одинаковую конфигурацию, позволяет вычислить сумму произведений одноименных элементов. Результат вычисления по формуле СУММПРОИЗВ(B3:E3;B4:E4) равен В3*В4+С3*С4+D3*D4+E3*E4,
 |
Рис.2.4. Исходные данные
2. Активизируем надстройку Поиск решения из пункта меню Сервис и заполним диалоговое окно, как это показано на рис.2.5 (в параметрах обязательно отметим линейность модели рис.2.6). Нажмем на кнопку Выполнить.
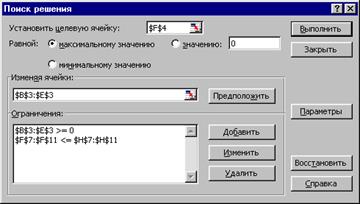
Рис.2.5. Диалоговое окно Поиск решения
3. На рис.2.7 показано полученное решение. При этом в ячейках диапазона B3:E3 находятся искомые значения объемов выпуска продукции, соответствующие оптимальному плану. В ячейке F4 находится значение целевой функции (ЦФ), которое соответствует этому оптимальному плану.

Рис.2.6. Параметры Поиска решения
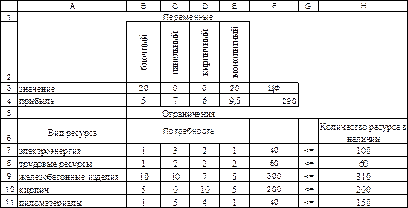 |
Дата добавления: 2015-09-03; просмотров: 111 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| ТЕМА: ЗАДАЧА О РАСПРЕДЕЛЕНИИ РЕСУРСОВ | | | Отчет по устойчивости. |