Сравнение стратегий управления запасами

Оптовик хочет сравнить преимущества и недостатки двух стратегий разме­щения заказов в условиях неопределенности спроса. Имеется два варианта по­литики размещения заказов:

(i) заказывать партии из 10 единиц товара при точке заказа 10;

(ii) заказывать партии из 15 единиц товара при точке заказа 15.

Уровень запасов проверяется в начале каждого дня.

В прошлом году дневной спрос на этот товар выглядел следующим образом:

Таблица 5
Дневной спрос:
Процент:

Имеется и другая дополнительная информация, а именно:

(i) Затраты на хранение запасов составляют 15 ф. ст. на единицу товара в

день.

(ii) Затраты на подготовку заказа составляют 50 ф. ст. на один заказ в виде административных издержек, транспортных расходов и расходов на упаковку.

(iii) Финансовые потери в результате утраты престижа фирмы оценивают­ся в 30 ф. ст. за каждое потерянное требование.

(iv) Поставка осуществляется в начале третьего дня с даты размещения заказа.

(v) Уровень запасов на начало первого дня составляет 17 единиц товара.

С помощью модели мы можем определить наиболее эффективную и эко­номную политику размещения заказов.

Для моделирования дневного спроса на этот товар можно взять двузначные случайные числа. Имеется 10%-ная вероятность спроса в 4, и это можно пред­ставить первыми десятью случайными числами (т. е. 00—09). Итак, в итоге по­лучаем следующую таблицу:

Таблица 6
Дневной спрос:
Процент:
Случайные числа:	00-09	10-24	25-49	50-79	80-99

С помощью таблицы случайных чисел, которую мы дали в начале этой главы, мы смоделируем спрос на данный товар. Далее в таблице приведена модель на 10 дней при размере и точке заказа в 10 единиц.

	A	B	C	D	E	F	G	H	I
	День	Уровень запасов на начало дня	Спрос	Продано	Уровень запасов на конец дня	Затраты на подготовку заказа	Затраты на хранение	Затраты вследствие дефицита	Всего затрат
			8(89)
			4(07)
			6(37)
			6(29)
		0(+10)	6(28)
			4(08)
			7(75)
		0(+10)	4(01)
			5(21)
			7(63)
		Итого				150 ф. ст.	930ф.ст.	600 ф. ст.	)680()),ci

Рис. 8

Значения в колонках таблицы получены следующим образом:

(i) Уровень запасов на начало 1-го дня составляет 17 единиц. Далее, начи­ная со 2-го дня, запасы на начало дня равны уровню запасов на конец преды­дущего дня. Исключение составляют дни, когда поступает новая партия. В этот день размер партии прибавляется (+10) к уровню запасов на начало дня и соответственно учитывается при расчете затрат на хранение запасов.

(ii) Спрос моделируется с помощью случайных чисел, взятых из ранее приведенной таблицы. Взятые случайные числа даны в этой колонке в скобках.

(iii) Объем продаж равен спросу при условии наличия достаточных запа­сов на начало дня. Если спрос превышает уровень запасов на начало дня, то объем продаж равен уровню запасов на начало дня.

(iv) Уровень запасов на конец дня равен уровню запасов на начало дня минус объем продаж плюс объем поступления.

(v) Затраты на размещение заказа составляют 50 ф ст. В этом примере заказы размещаются тогда, когда уровень запасов достигает 10 или менее еди­ниц. Новая партия из 10 единиц поступает на третий день с даты размещения заказа и прибавляется в день поступления к уровню запасов на начало дня

(vi) Затраты на хранение запасов рассчитываются путем умножения уров­ня запасов на начало дня на 15 ф. ст. (В уровень запасов на начало дня включа­ется поступление новой партии, если таковое происходит в этот день)

(vii) Любое неудовлетворенное требование обходится компании в 30 ф ст Количество потерь требований в течение любого дня рассчитывается как разни­ца между спросом и уровнем запасов на начало того дня, когда спрос превы­шает уровень запасов на начало дня. То есть затраты вследствие дефицита рас­считываются путем умножения этой разницы на 30 ф ст

(viii) Общие затраты рассчитываются путем сложения значений трех пре­дыдущих показателей: затрат на подготовку заказа, затрат на хранение и потерь вследствие дефицита.

Как видно, смоделированная в этой таблице политика размещения заказов не является эффективной. Имеется большое количество потерь требований При спросе в 57 единиц объем продаж за указанный период составил только 37 единиц. Это, скорее всего, неприемлемо в большинстве случаев независимо от других затрат.

А теперь рассмотрим ту же самую модель при другой политике размещения заказов, когда размер партии составляет 15 при точке заказа 15. В таблице при­ведена эта модель (спрос остался прежним):

	A	B	C	D	E	F	G	H	I
	День	Уровень запасов на начало дня	Спрос	Продано	Уровень запасов на конец дня	Затраты на подготовку заказа	Затраты на хранение	Затраты вследствие дефицита	Всего затрат
			8(89)			—		—
			4(07)					—
			6(37)			—
			6(29)			—	—
		0(+15)	6(28)					—
			4(08)			—		—
			7(75)			—
		0(+15)	4(01)					—
			5(21)			—		—
			7(63)			—
		Итого				150 ф ст	1380ф ст	300 ф ст	1830 ф ст

Рис. 9

Из этой таблицы видно, что новая политика размещения заказов лучше. В частности, при этой политике меньше потерь требований' при спросе в 57 единиц объем продаж составил 47 единиц В целом уровень запасов выше, а отсюда выше и затраты по хранению (всего 1380 ф. ст. по сравнению с преды­дущим итогом в 930 ф. ст.). И наоборот, вследствие более высокого уровня запасов реже возникает дефицит, и поэтому меньше потери вследствие дефи­цита (сравните 30 ф. ст. с 600 ф. ст.). Вместе с тем при новой политике возросли общие затраты (сравните 1830 ф. ст. и 1680 ф ст.) На первый взгляд, получается, что исходная политика лучше. Однако в модели не учитывается фактический доход от реализации этих товаров, и если мы это учтем, то вполне вероятно, что политика заказа партиями по 15 единиц окажется более эффективной Так, за десятидневный период объем продаж вырос с 37 до 47 Если единица товара приносит 200 ф. ст., то в указанный период доход вырос на 2000 ф ст Это компенсирует небольшие дополнительные затраты на хранение запасов. С дру­гой стороны, если единица товара приносит только 2 ф. ст. дохода, то тогда, возможно, необходимо изменить политику.

Из этих аргументов следует, что при анализе результатов моделирования необходимо проявлять осторожность. Но при этом очевидно, что полученные модели дают четкое представление о процессах и могут помочь руководителю выработать наиболее приемлемую политику размещения заказов при наличии определенных условий. Далее можно провести моделирование затрат при раз­личных значениях запасов. Так, в таблице показаны общие затраты (в ф. ст.) в течение двадцатидневного периода при различных значениях размера и точки заказа. Во всех случаях использовалась одна и та же последовательность из двад­цати значений спроса:

Таблица 7
Точка заказа	Размер заказа (партии)

Из этой таблицы видно, что размер заказа в 10 единиц при точке заказа в 5 единиц минимизирует общие затраты. То есть такой вариант можно предложить в качестве оптимально возможного решения данной задачи по размещению заказов. Но вполне вероятно, что это связано с относительно высокими затратами на хранение (15 ф. ст. на единицу в день). Это означает, что затраты удерживаются на низком уровне за счет простого удержания запасов на минимуме. Однако при такой низкой точке заказа есть вероят­ность того, что большая часть требований не будет удовлетворена. Для боль­шинства поставщиков такое положение вещей обычно абсолютно неприем­лемо. Более четкое представление об эффективности этих стратегий можно получить путем сопоставления прибыли за тот же самый период. В таблице ниже приведены значения числой прибьши при условии, что единица това­ра приносит валовую прибыль в 100 ф. ст. (без учета затрат на хранение, приведенных ранее):

Таблица 8
Размер заказа (партии)
Точка заказа

И вновь, значения в этой таблице получены с помощью той же самой последовательности произвольно выбранных значений спроса. При других значениях мы бы получили другие результаты. Но они были бы похоже на те, что мы имеем в этой таблице. Для получения более реалистичной оценки ожидае­мой прибыли в каждом случае можно взять среднее значение по результатам нескольких прогонов модели. Тем не менее эта таблица все же указывает на возможные решения данной задачи максимизации прибыли. Видно, что размер заказа в 15 единиц дает относительно постоянный уровень прибыли для целого диапазона точек заказа.

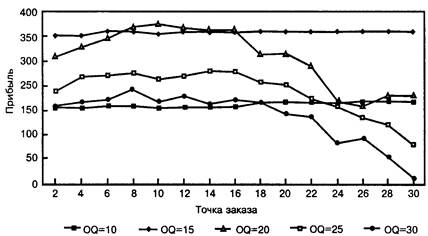
Рис. 9.2. Средняя дневная прибыль

Это неудивительно, так как такое количество наиболее близко к среднему спросу за три дня, что соответствует циклу заказа по этому товару.

Эти значения можно отобразить на графике, чтобы показать влияние раз­личных значений на размер и точку заказа. На рис. 9.2 дано дальнейшее моде­лирование этой ситуации на протяжении 100 дней. На графике отображена среднедневная прибыль, полученная при моделировании продаж в течение 100 дней при различных значениях двух переменных: по горизонтали показана точ­ка заказа, а по вертикали — значения среднедневной прибыли. Линии представ­ляют ряды значений для различных размеров заказа. Из графика видно, что размер заказа в 15 единиц дает устойчивую линию с небольшими отклонени­ями в зависимости от значения точки заказа. Но из графика также следует, что размер заказа в 20 единиц увеличивает размер прибыли, особенно при точке заказа в 10 единиц. Чтобы подтвердить эти результаты, необходимо проработать новые модели с другими значениями спроса.

9.9. Упражнения: модели управления запасами

1. (Е) С помощью случайных чисел смоделируйте спрос на товары в тече­ние 10 дней. Спрос распределен следующим образом:

Таблица 9
(i)	Спрос:
	Процент:
(ii)	Спрос:
	Процент:
(iii)	Спрос:
	Процент:

2. (i) Магазин электротоваров «АВС» в Нью-Йорке реализует различные электротовары, в том числе системы Hi-Fi, проигрыватели лазерных дисков, стиральные машины и холодильники. Дневной спрос на стиральные машины «Электролуп де-люкс» распределен следующим образом:

Таблица 10
Дневной спрос:				4 5
Процент				20 5

Запасы обычно пополняются при достижении уровня в 6 единиц и менее, при этом размер заказа составляет 8 стиральных машин, а цикл заказа — 3 дня.

При условии, что первоначальный запас составляет 10 стиральных машин, определите с помощью метода моделирования спрос на этот товар в течение 20 дней. Какова вероятность возникновения дефицита при проведении такой по­литики размещения заказов?

3. (D) Рассмотрим задачу из п. 2. Но введем дополнительную информацию:

а) Стиральные машины продаются в розницу по цене 300 долл. США за штуку.

б) Стоимость приобретения у производителя одной машины составляет 150 долл..

в) Затраты на оформление заказа составляют 50 долл. на один заказ в виде административных издержек и расходов по доставке.

г) Неудовлетворенная потребность обходится «АВС» в 200 долл.

(i) Повторно смоделируйте ситуацию, как в п. 2, но с учетом дополни­тельной информации. Определите дневные доходы и расходы, связанные с реализацией стиральных машин.

(ii) He лучше ли заказывать по 10 машин в одной партии при точке заказа в 8 или менее? Отработайте этот вопрос на новой модели.

(iii) Как насчет других стратегий размещения заказов? Что если компании заказывать по 20 машин при точке заказа от 10 и ниже? Смоделируйте эту ситуацию на отрезке в 10 дней, чтобы показать, почему такая стратегия, ско­рее всего, неразумна.

Дата добавления: 2015-09-03