Норм напряж при изгибе

При плоском попер изгибе в кажд точке попер сеч балки возник норм и касат напряж.

Устан связь между напряж и внутр усилиями.

Попер силой Q наз равнод всех внутр касат сил в попер сеч

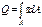
Изгиб мом М_х наз результир мом всех внутр норм сил действ в попер сеч.

Эпюра распред норм напряж в попер сеч.

Устан, что нейтр линия проходит через ц.т. сеч. Ось симметрии так же явл нейтр линией.

1) симметричное сеч:

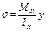
Из ф-лы видно: если у = 0 => σ = 0, у = у _тах => σ = σ _тах

2) несимметричн сеч относ н.о.:

Вывод: на нейтр линии норм напряж в сеч = 0, а в точках наиб удал от нейтр оси σ _тах.

Ф-лу можно предст в др виде

- осевой мом сопротивления

тогда ф-ла для опред напряж:

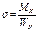- для симм-ных сеч, заключ в прямоуг(, двутавр, ][).

Осевой мом сопр (W_x) наз отнош осевого мом инерции к расст от н.о. до наиб удал точки.

25)

В попер сеч балки в этом случае возник попер сила и изгиб мом. Наличие попер силы связано с возникн касат напряж в попер и прод сеч балки.

Попер сеч после деф не только повёрн на некот угол, но и изогнулись. Причём их искривление наибольшее у н.о. Искривление произошло за счёт сдвига вызван касат напряж. Поскольку сдвиг не изменяет длины, то ф-лой для опр норм напряж:

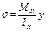- Можно польз и для попер изгиба.

Вел-на касат напряж в люб точке попер сеч опред по ф-ле Журавского:

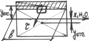
Q – попер сила рассм в сеч

b – ширина сеч в том месте, где опр касат напряж

I_x – осевой мом инерции

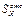- статический мом относ н.о. части площади сеч располож выше или ниже того уравня, где опр касс напряж.

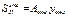
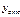- расст от ц.т. отсечён части до н.о.

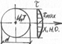
Распред касат напряж по высоте сеч балки

Для т. В:

При перемещ т. В вверх 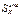уменьш и в т. В’ 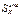= 0

(т.к. А _отс = 0) => τ = 0.

На н.о. 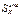= тах = 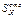_тах => τ _тах.

Знак касат напряж опр только знаком попер силы Q, 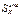берётся по абсолютной вел-не. Наиб касат напр для сеч типа □, ○, двутавр возник на н.о. и опр по ф-ле:

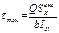В т. А, где соед полка со стенкой резко измен-ся ширина сеч по этому τ тоже будет измен-ся.

Дата добавления: 2015-09-03