Определение внутренних сил

Прод-ая сила N опр-тся методом сечения. Намечаются уч-ки бруса, границей уч-ка явл-ся точки приложения сил. Рассечём уч-к пл-тью и мысленно отбросим одну часть бруса. В сечении прикл-ют прод-ую силу направим её в сторону отбр-ной части, т.е. предположим, что N – растяг-ей сост-щей ур-ия равновесия: сумма всех сил на OZ = 0, из кот опред-ся N. Прод-ая сила N, численно равная алг-кой сумме внешних сил, распол-ых по одну сторону от сечения..

Что бы наглядно видеть места с наиб-им N строится эпюра, это график показ-ий изм-ие того или иного фактора по длине бруса.

5) По усилию нельзя судить о прочности стержня.

Определение нормальных напряжений (σ) в поперечном сечении

Рассм-им растянутый стержень:

В сечении выделим элем-ую площадку dA, по ней действ-щее напряжение σ:

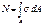
Для нахождения напряжения ур-ий статики не достаточно, необх знать з-н распред напряжения в поперечном сечении.

Прибегнем к эксперименту на пов-ть образца нанесём ряд ║ линий, увидим, что после деф поперечные линии не искривились и все точки по высоте сечения переместились на одну и туже вел-ну. Можно предположить, что такая же картина происх и в нутрии тела, т.е. плоские попер сечения до деф остаются плоскими и после деф. Эта гипотеза плоских сечений или гипотеза Бернулли. Из этой гипотезы следует, что и нормальное напряжение по высоте сечения остаются постоянными.

σ = const

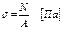-нормальное напряжение при прод-ом растяж-сжатии

При расчете напряжения также используется принцип Сен-Венона: «Напряж состоян тела на достаточно удален от облости действия нагрузок очень мало зависит от детального способа прилож этих нагрузок

Дата добавления: 2015-09-03