Механические характеристики материалов

Мех хар-ки м-ла необх для расчётов эл-тов констр на прочность и жёсткость. Основным опытом для получения мех хар-к для пластич-их м-лов явл-ся испытание на растяжение. Изгот-ся станд-ые образцы, у кот отношение расчётной длины l_o к диаметру поперечного сечения d_o = 10. Машина автом-ки записывает диаграмму зависимости между растяг-щей силой F и удлинением образца ∆ l.

Диаграммы перестраивают в др виде, по оси ординат – нормальное напрчжение σ = N/A_о (A_о – первонач-ая площадь попер сеч образца), по оси абсцисс – относ-ое удлинение ε = ∆ l/l_o. Эту диагр наз диагр-мой условных напряжений, т.к. A_о – постоянной применяется в процессе удлинения.

1 – σ_pr – предел прямо пропор-ти

1’ – σ_e – пр упругости

2 – σ_y – пр текучести

3 – σ_u - пр прочности

По диаграмме опред-ся мех хар-ка прочности образца: На уч-ке 0-1 деф-ции растут проп-но нагрузке, т.е. вып-ся закон Гука. 1 – предел проп-ти – наиб-ее напряж, для кот спроведлив з-н Гука. Уч-к 0-1’ – м-л испыт-ет только упругие деф-ции (ε_е). 1’ – предел упругости – наиб напряж, после кот возние-ет остат-ые деф-ции (ε_r). Если нагрузку увелич-ть дальше, то наступит такой момент, когда напряж не увелич-ся, а деф-ция всё равно растёт (1’ – 2). Гориз уч-к – наз площадкой текучести, а состояние м-ла – текучестью. Самая низкая точка на площадке текучести соотв-ет пределу текучести. На этом уч-ке диагр на отполированной пов-ти образца появл-ся очень маленькие трещины (линии сдвигов – линии Людерса-Чернова), они наклонены к оси образца на 40 -50⁰. Претерпев состояние тек-ти м-л снова приобретает сп-ть сопротивляться нагрузке, как бы упрочняться, и диаграмма опять идёт вверх. Предел прочности (σ_u) – наиб напряж, кот может выдержать м-л без признаков разрушения. В 3 на образце появл-ся – т.н. шейка – местное сужение попер сечения образца. Площадь сеч в шейке быстро уменьшается, напряж падает и в точке 4 происходит разрыв образца.

12)

13) Необходимые размеры сечений элементов конструкции определ из расчетов на прочность, жесткость и устойчивость. Расчеты на прочность свод к требованию, чтобы наибольшее напряж в элементе конструкции не превосходят некоторой допустим величины. Существует 3и метода расчета на прочность.

1ый- допустимых напряжений

2ой-предельных состояний

3ий-разрушающих нагрузок

Метод допустимых напряжений требует выполнение 2ух условий σ_p ≤ [σ_p] σ_с ≤ [σ_с] или σ ≤ [σ], где σ- наибольшее по абсолют величине сжимающее или растягивающее расчетное напряжение для материала, [σ]= σ_т/ [n_т]; σ_p иσ_с– наибольшие расчетые напряжения, [σ_p] и [σ_с]- допустимыенапряжения.

Нагрузка, при которой наибольшее напряжение в конструкции равны допускаемым напряжениям, называется допускаемой.

Метод предельных состояний. В данном случае допустим нагрузку назыв предельно допускаемой нагрузкой, а ее величину определяют путем деления предельной нагрузки на нормативный коэффициент запаса несущей способности. Следует стремиться к тому, чтобы допускаемые напряжения были полностью использованы, т.е. удовлетворять условию σ = [σ]

Метод разрушающих нагрузок заключаетсяв том чтобы определит максимальные сжимающие и растягивающие напряжения.

14) Необходимые размеры сечений элементов конструкции определ из расчетов на прочность, жесткость и устойчивость. Расчет на жесткость сводиться к требован чтобы наибольш перемещение не превышает допустимой величины.

15) Статический момент плоской ф-ры

Предполож имеем сечение площадью А. выделяем элем-т участок dA. Статич момент относ любой оси х или у назыв сумма произвед элем-ых площадок на рассм до соотв оси.

;

Покажем центр тяжести сечения и его к-т.Точка пересечения осей Х и У и есть центр тяжести сечения.

Координаты центра тяжести находятся из формул у_с= /А и x_с= /А

Если известно полож ц.т. фигуры, то статический момент опред-ся: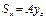

Статич момент относит оси, кот проходит через ц.т. равны 0. Оси воторые проходят через центр тяжести называбтся центральными осями. Размер-ть S_x, S_y – см³

Статич момент для сложн ф-ры равен сумме статич мом-ов всех сост-щих частей.

;

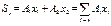
Используя запись выраж и определ ц.т. сплошной ф-ры.

;

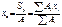16) Осевым моментом инерции сечения относительно некоторой оси называется взятая по всей его площади А сумма произведений элементарных площадок dA на квадраты их расстояний от этой оси, т.е.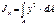

Полярным моментом инерции относительно неторой точки (полюса) называется взятая по всей его площади А сумма произведений элементарных площадок dA на квадраты их расстояний от этой точки, т.е.

Центробежный момент инерции сечения относительно некоторых 2ух взаимно перпендекулярных осей называется взятая по всей его площади А сумма произведений элементарных площадок dA на их расстояния от этих осей, т.е.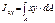

Моменты инерции имеют размерности см⁴, м⁴.

Осевые и полярные момениы всегда положительны, т.к. величины входящие в их вычисления положительны и расстояния в вычислениях беруися в квадрате.

Сумма осевых моментов инерции сечения относительно 2ух взаимно перпенд осей равна полярному моменту инерции этого сечения относительно точки пересечения указанных осей.

Центробежн моменты могут быть +, - и =0

Центробежн момент инерции сечения относительно осей, из которых одна или обе совпадают с его осями симметрии, равен 0.

17)

Момент инерции относительно любой оси, кот ║ центральной.

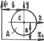Найдём момент инерции относ осей х₁, у₁, кот ║ х, у и отстают от заданных осей на расст a, b.

;

Момент инерции относ любой оси равен инерции относ центральной оси плюс произведение площади на квадрат расст между осями.

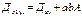
Момент инерции относительно осей, повёрнутых на угол α.

Если известен мом инерции относит двух взаимно ┴ осей ху, то мом инерции относ осей х₁ у₁, повёрнутых на угол α по отнош к исходным, вычисл по ф-лам.

Доказываемо, что сумма мом инерции при повороте осей не мен, т.е. const.

I_x + I_у = I_x1 + I_у1

При повороте осей один из мом инерции увеличив, другой уменьшается. М. найти такое полож осей, при кот мом ин приним экстремальное знач (одно наиб, др наим-шее). Центробежный мом ин относит этих осей равен 0. Такие оси наз главными.

Положение гл центр осей опред-ся по ф-ле:

Если уг α_о > 0, то он откладыв от оси х против хода часовой стрелки (вверх). Если α_о < 0, то отклад по ходу часовой стрелки (вниз).

u → (I_x > I_y); v → (I_x < I_y)

v (I_x > I_y); u (I_x < I_y)

18) Экстремальные значения осевых моментов инерции сечения называются главными моментами инерции. Оси относительно, которых осевые моменты инерции имеют экстремальные значения, называются главными осями инерции. Главные оси можно провести через любую т-ку сечения, но в сопротивлении м-лов наиб-ший интерес представляет главные оси, проходящие через ц.т. сечения. Такие оси наз главными центральными осями. Мом инерции относ главных центр осей наз главными центр-ми мом-ми инерции.

Т. обр. гл-ми центр-ми осями наз оси, обладающие след-ми св-вами:

1) проходят через ц.т. сечения.

2) центробежный мом инерции относит этих осей равен 0.

3) мом-ты инерции относит этих осей принимают экстремальное значение.

Главные центральные оси обозначают u,ν.

Главные центраб мом инерции – I _u (max), I _ν (min).

Главные центр мом-ты инерции выч по ф-ле

Положение гл центр осей опред-ся по ф-ле:

Если уг α_о > 0, то он откладыв от оси х против хода часовой стрелки (вверх). Если α_о < 0, то отклад по ходу часовой стрелки (вниз).

u → (I_x > I_y); v → (I_x < I_y)

v (I_x > I_y); u (I_x < I_y)

Для симметричных ф-р можно сразу провести гл центр оси, одна гл совпад с осью симметрии, а вторая ей ┴ и проходит через центр тяжести сечения.

Радиусом инерции сечения относительно некоторой оси назыв величина определ из равенства

, где i-радиус инерции

19)

Построим на главных центральных осях инерции фигуры эллипс с полуосями, равными главным радиусам инерции, причем вдоль оси откладываем отрезки , а вдоль оси — отрезки

Такой эллипс, называемый эллипсом инерции, обладает следующим свойством. Радиус инерции относительно любой центральной оси определяется какперпендикуляр проведенный из центра эллипса на касательную, параллельную данной оси. Для получения же точки касания достаточно провести параллельно данной оси любую хорду. Точка пересечения эллипса с прямой, соединяющей центр О и середину хорды, и есть точка касания. Измерив затем отрезок ,находим момент инерции

Круг инерции представляет собой геометрическое место точек, координаты которых в осях построения определяют осевые и центробежные моменты инерции площади относительно любой пары взаимно перпендикулярных осей, проводимых через данную точку.
Чтобы построить круг инерции, надо располагать значениями трех исходных величин - моментов инерции относительно пары прямоугольных координатных осей, проходящих через заданную точку.
С помощью круга инерции можно графически определить моменты инерции относительно произвольных осей. При этом обычно строят круг инерции по известным моментам инерции Jx, Jy, Jxy, вычисленным относительно произвольных осей Ох и Оу

Дата добавления: 2015-09-03