Плоское н.с.

Имеет место, когда на эл-т действ 2-а гл напряж.

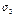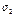= 0, = 0

Примером является изгиб.

Опред норм и касат напряж по наклон площадкам.

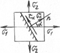
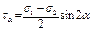
Анализ ф-л показал:

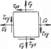α = 0, , 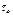= 0 (гл пл-дь)

α = 45⁰: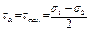

α = 90⁰: 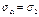, 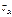= 0 (гл площ).

На практике часто приходится реш обратную задачу, т.е. опред главн напряж по известным неглавным.

Главные напряж опред по ф-лам:

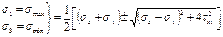
Полож гл пл-к опр по ф-ле:

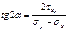
Если , то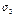

Если , то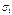

32)

Паралле-д выделен из тела должен находится в равновесии под действием сил прилож к его грани сила прилож к грани должна быть уравновеш такой же силой на противоположной

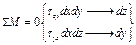
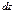где площадь грани, а плечо

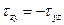- закон прочности касат напряж

33)

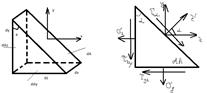
Все силы проецируем на 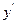и

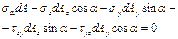
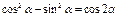
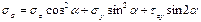
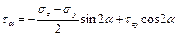
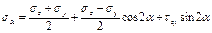
Сделаем 1-ое сеч под углом α к попер сеч, 2-ое ┴ сеч 1-ому.

n – нормаль

Нормальн и касат напряж по накл сеч опр по ф-лам:

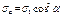
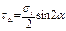
Где уг α отсчит от напр σ₁ против час стрелки. Напряж по площадке под углом (α + 90^о) опред по ф-лам:

Заметим, что - з-н парности касат напряж:

«Касат напряж по двум взаимно ┴ площ-кам = по вел-не и противоп по знаку».

Т.к 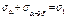, то делаем вывод, что сумма норм напряж по двум взаимно ┴ площ-кам не изменяется и = гл напряж.

34)

На площадку где действуют экстримальные нормальные напряжения, касательные напряжения равны 0, такие площадеи называются главными площадками, а напряжения действующие на главных площадках называются главными напряжениями.

=0

Согласно данной формуле мы получаем 2а взаимно перпендикулярных наклона по которым действуют главные напряжения

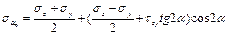
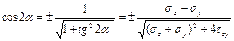
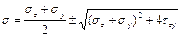
σ_{max c +,а} σ_{min c -}

35) Одно и тоже плоск напряж сост в точке может быть представл различными напряж площ и напряж, т.к. касат напряж на главных площадках отсутствуют, то главн площ и напряж наиболее просто определить напряж сост в точке.

Экстрим касат напряж в точке равны полуразности главных напряж и действ по площ наклон к главным на угол 45

Определим максимальн напряжения

В частном случаи, когда на гранях элемента действ численно равн растягив и сжим напряж 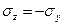, то экстрим касат напряж будут равны

36)

37)

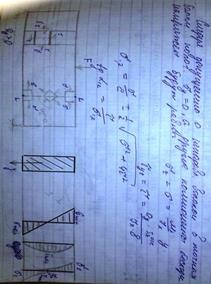
Траектории главных напряжений, так назыв линии в каждой точке которой касат совпадает с направл главных напряжений в этой точке.

При простом растяжен груза траектория главн напряж яал прямые параллельные и перпендикулярные его оси.

Если во всех точках скручивоемого стержня,,, направления главных напряж, то на поверхности получим сетку взаимно ортоганальных кривых пересек образующ под углом 45

Для получения троектории в изгиб балке используем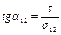

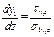
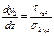где у1 и у2 ординаты троектории σ1и σ2 соответственно

Эти уравнения интергрируются и определ у1 и у2

38)

Как в плоском так и в объемном напряж сост линия ориентирования паралле-да можно определить такое его напряж при котором на всех его гранях касательные напряжения будут равны 0. Такие площади будут называться главными и напряжения тоже главными

Суммы прекций на оси раны 0. Из этого

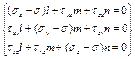
l²+m²+n²=1

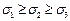
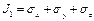
J не зависит от выбора координатных осей.

39)

Если мысленно вращать оси х,у и z относительно точки М приводя их во всевозможные положения, то их деформация будет изменяться.

Совокупность относительных удлинений и углов сдвига для всевозможных направлений осей проведеных через данную точкуназывается деформир сост в точке.

Деформации для которых отсутствуют углы сдвига называются главными деформациями и для главных направлений тензор деформации будет иметь вид

Компоненты тензора деформ при повороте осей измен аналогично компонентов тензора напряжения. Выражение для главной относительной деформации

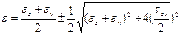
40)

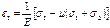
В случаи если одно из напряжений =0, то получим плоское напряж сост. И з-н Гука для такого сост будет выглядеть следующим образом

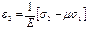
Если 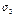=0 то это не означает что 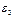=0

Для главных площадок где касат напряж не равны 0 формулы связ σ и 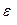имеют вид

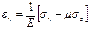
41)

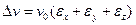абсолютное изменение объема параллепипеда

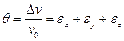
42)

Для прост напряж сост удельная потенц энергия

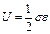
Для обобщ случ когда имеем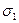

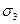
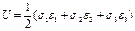
Если грани кубика не явл главн площ и на их грани действ нормальные и касательные напряжения, то потенц энергия =

43) Деф сдвига наблюд в тех случ, когда силы F пытаются сдвинуть (срезать) одну часть элемента констр по отнош к другому, и в поперечном сечении возникает только одна внутр сила – поперечная сила Q.

Чистым сдвигом называется такой вид плоского напряж и деформ сост. при котором на 2ух взаимноперпенд площ ориент опред образ действ только касат напряжен Указаные площади назыв площ чистого сдвига.

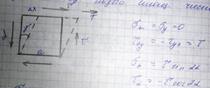
σ->0 при α=0 или при α= 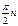на всех других площадях σ≠0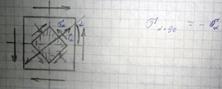

З-н Гука при сдвиге:

Эксперементально изучен деформ чистого сдвига проводят путем кручения трубчатых образцов

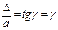относит сдвиг, 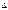абсол сдвиг

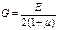Для многих материалов предел текучести при сдвиге связ с σ_текпри растяж с след соотношен τ_т=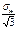

44)Практические расчёты на сдвиг

1. Заклёпочные соединения

Заклёпки расчит на срез и смятие, а соединяемые листы элемента на растяж, сжатие по ослабленному сечению.

t_л – толщина листа; d – диаметр заклёпки

Условие прочности на срез (заклёп соед)

n – кол-во заклёпок в соединении

n_cp – кол-во плоскостей среза заклёпки

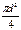- площадь среза 1-ой заклёпки

Условие прочности на смятие (заклёп соед)

Передача усилия от листа к заклёпке происходит по цилиндрической пов-ти к заклёпке.

З-н Распределения напряжений по пов-ти заклёпки сложный и пока не изучен.

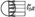Условно принимаем 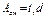, также будем считать, что напряж распред равномерно по диаметру заклёпки.

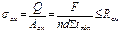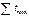; - наименьшая суммарная толщина эл-тов соединения, кот сминают заклёпку в одном направлении.

Используя условие прочности на срез и смятие расчит кол-во заклёпок, диаметр и усилие соединения.

Условие прочности на растяжение соединяемых элементов (заклёп соед)

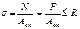
- площадь сечения ослабленного заклёпочным отверстием.

2. Сварные соединения.

1) Сварка встык

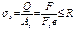- усл прочн на раст электрошва

Сварные швы встык расчит на растяж.

А_Э – толщина электрошва

R_Э– расчётное сопрот на растяж эл-кого шва

2) Сварка в нахлёстку

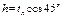
Разрушение эл-кого шва происходит под углом 45^о к катету шва и условие прочности на срез:

L – длина всего электрошва

R_э – расчит сопр на срез эл шва

45)Кручение - такой вид деф, когда в попер сечении эл-та констр возник 1-а внутренняя сила – крутящий момент (М_к).

Кручению подверг многие детали машин и механизмов. Кручение прямого бруса происходит при нагружении его внешними закручивающ моментами (т), действ-щими ┴ к продольной оси бруса.

Дата добавления: 2015-09-03