Включение R, L, C цепи на постоянное напряжение

Дано: R, L, C, U

Определить: U_c(t), i(t), U_R(t), U_L(t)

1) Начальные условия до коммутации:

U_C(0_-)=U_C(0₊)=0

i(0_-)=i(0₊)=0

2) Составляем дифференциальное уравнение:

U_R+U_C +U_L =U

(1)

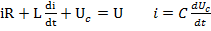
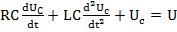– дифф. уравнение 2 порядка.

(2)

3) Решение дифференциального уравнения:

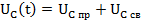
U_{c пр} =?

U_{c пр} = U

U_{c св} =? – общее решение однородного уравнения.

LC p² + RC p + 1 = 0

Возможны 3 случая из-за выражения под корнем:

1) Апериодический режим переходного процесса:

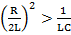, p_1,2 – вещественные и разные.

2) Критический режим переходного процесса:

, p_1,2 – вещественные и одинаковые.

3) Колебательный режим переходного процесса:

, p_1,2 – комплексные и сопряженные.

Апериодический режим.

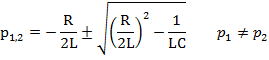
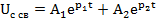
(3)

(4)

A₁, A₂ – определяем из начальных условий.

U_C(t)|_t=0 = 0 = A₁+A₂+U

i(t)|_t=0 = 0 = A₁p₁ +A₂p₂

Из системы уравнений определяем A₁, A₂ - например, методом определителей.

– берем производную от (4)

U_R = iR

---

Дата добавления: 2015-08-21