Решение уравнения (1)

i(t)=i_св+i_пр = i_пр+Ae^pt = i_пр+Ae^-t/τ

i_св = i_св – находится как в предыдущих случаях.

i_пр -? Определяем символическим методом.

i(t)=i_св+i_пр=I_msin(ωt+α_u-φ)+ Ae^-t/τ

A=?

i(t)|_t=0 = 0 = I_msin(α_u-φ)+ Ae⁰ => A= -I_msin(α_u-φ)

i(t)= 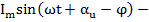I_msin(α_u-φ) e^-t/τ

Частные случаи:

1) Переходный процесс отсутствует

α_u-φ=0

sin(α_u-φ)=0

2) Максимальный переходный процесс

sin(α_u-φ)= ±1

α_u-φ = ±π/2

Пусть α_u-φ = π/2

i(t)= 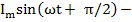I_m e^-t/τ

I_mR sin(α_u-φ) e^-t/τ

7.3.4| Включение R, C цепи на постоянное напряжение.

Дано: R, C, U.

Найти: U_c(t), U_R(t), i(t).

1) Н.У. до коммутации:

U_C(0_-)=U_C(0₊)=0

2) Схема после коммутации:

U_R+U_C=U

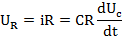
U_R=U

(Дифференциальное уравнение 1 порядка.)

3) Решение дифференциального уравнения:

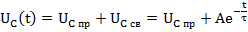
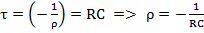– Корень характеристического уравнения.

U_{c пр}=?

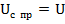
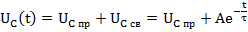
A=? – ищем из начальных условий.

U_c(t)|_t=0 =0=U+Ae⁰ => A = -U

, где τ=RC

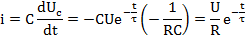
7.3.5| Короткое замыкание R, C цепи.

Дано: R, C, U.

Определить: U_c(t), i(t), U_R(t)

U_c+U_R=0

Будет разрядка конденсатора:

U_{с пр} = 0

U_{с св} = Ae^-t/τ

A=?

U_c(t)|_t=0 = U = Ae⁰ => A=U

U_c(t)= Ue^-t/τ

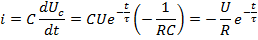
U_R=iR= -Ue^-t/τ

7.3.6.| Включение R, C цепи на синусоидальное напряжение

Дано: R, C, U(t)=U_msin(ωt+α_u)

Определить: U_c(t), i(t), U_R(t)

1) Начальные условия до коммутации:

U_C(0_-)=U_C(0₊)=0

2) Схема после коммутации:

U_R+U_C=U_m sin(ωt+α_u)

iR+U_C=U_m sin(ωt+α_u)

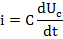
(1)

3) Решение дифференциального уравнения (1):

, где τ = RC

U_{c пр}=?

– комплексная амплитуда.

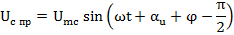
A=? – постоянную интегрирования определяем из начальных условий.

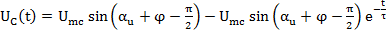(2)

(3)

U_R = i R (4)

Рассмотрим предельные случаи для выражения (1):

1) Переходный процесс отсутствует, если

2) Максимальный переходный процесс

3) Аргумент равен –π/2

Дата добавления: 2015-08-21