Графоаналитический метод разложения функции в ряд Фурье

Графоаналитический метод разложения в ряд Фурье представляет собой приближенный метод численного интегрирования, при котором вычисление определенного интеграла заменяется нахождением суммы конечного числа слагаемых. С этой целью период функции f(a) разбивается на m равных интервалов Δa так, что mΔa=2π.

Рассмотрим три случая разложения в случаях симметрии:

1) Случай парабол.

Функция f(x) симметрична относительно оси ординат, т.е. f(x) = f(-x) - четная функция. Поскольку синусоиды любых частот являются нечетными функциями, они не входят в состав ряда. Поэтому при данном виде симметрии:

Т.е. четная функция может содержать только косинусоиды и постоянную составляющую.

2) Случай прямоугольников.

Функция f(x) симметрична относительно начала координат, т.е. f(x) = -f(-x) - нечетная функция. Поскольку постоянная слагающая и косинусоиды этому условию не удовлетворяют, то при данном виде симметрии ряд примет вид:

Т.е. четная функция может содержать только синусоиды.

3) Случай трапеций.

Функция f(x) симметрична относительно оси абсцисс при совмещении двух полупериодов во времени.

Заменяя f(x), получаем:

Откуда для четных n

Это условие удовлетворяется при произвольных значениях x только в том случае, если а₀ =0 и a_n = b_n = 0 при четных n.

Поэтому при данном виде симметрии:

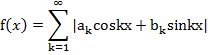
Т.е. функция, симметричная относительно оси абсцисс при совмещении двух полупериодов во времени, сожержит только нечетные гармоники.

Графоаналитическое определение действующего значения:

U(t) с периодом Т.

Вычислим интеграл приближенно по методу прямоугольников. Разделим Т на n равных частей, (k – номер высшей гармоники в ряде Фурье). Для t₁…t_n находим значения функции u(t₁), u(t₂)… Возводим их в квадрат.

---

Дата добавления: 2015-08-21