Индуктивность в цепи синусоидального напряжения

Дано: u=U_msin(ωt + α_u)

u→i→ψ→Li

ψ – Потокосцепление.

(А = 0, т.к. в установившемся режиме синусоиальный ток не имеет постоянной составляющей).

В индуктивности ток отстает от напряжения на .

Векторные диаграммы:

Когда p_L>0, энергия потребляется от источника и запасается в магнитном поле индуктивности.

Когда p_L<0, энергия возвращается обратно к источнику.

t →i(t) di=i’(t)dt

i(0) = 0 i(t) = i

Реальная катушка обладает еще и внутренним сопротивлением.

Векторная диаграмма:

4.4.3.| Емкость в цепи синусоидального тока

Дано:

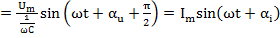
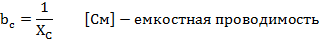
t →u(t) du=u’(t)dt

u(0) = 0 u(t) = i

Реальный конденсатор обладает проводимостью g, учитывающей потери в диэлектрике.

Чем выше добротность, тем меньше δ и ближе реальный элемент к идеальному.

δ – угол диэлектрических потерь – зависит от сорта диэлектрика.

δ= 1^’’ ÷ 1⁰

4.4.4| Последовательное соединение R, L, C

Дано:

Найти:

Решение:

По 2 закону Кирхгофа:

Заменим сложение синусоидальные напряжения сложением их векторов.

U_mp – реактивная составляющая.

U_mR – активная составляющая.

Такая векторная диаграмма называется треугольником напряжений.

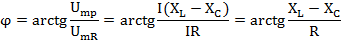
X = X_L – X_C – реактивное сопротивление цепи.

При X>0 в цепи преобладает индуктивный характер сопротивления φ>0.

При X<0 в цепи преобладает емкостной характер сопротивления φ<0.

При X=0, φ=0 – возникает резонанс напряжений.

Закон Ома для последовательной R, L, C цепи:

– импеданс, или полное сопротивление цепи.

Если треугольник напряжений разделить на ток, получим треугольник сопротивлений.

4.4.5| Параллельная R, L, C цепь

Дано:

R(g), L, C

Определить:

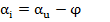
Решение:

Осталось найти I_m, φ.

Заменим сложение трех синусов сложением трех векторов.

– реактивная проводимость цепи.

Если b_L > b_C (b > 0, φ > 0) в цепи преобладает индуктивный характер проводимости.

Если b_L < b_C (b < 0, φ < 0) в цепи преобладает емкостной характер проводимости.

Если b_L = b_C (b = 0, φ = 0) в цепи резонанс токов.

Закон Ома для параллельной R, L, C цепи:

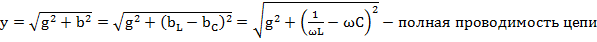
Если Δ такой цепи разделить на U_m, получим Δ проводимостей.

Дата добавления: 2015-08-21