Метод узловых токов

Определяют потенциалы узлов, затем через потенциалы считаются токи.

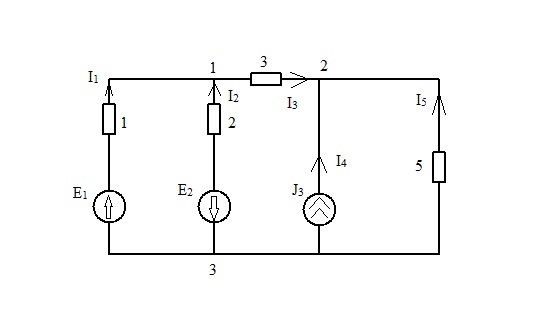Число уравнений в методе узловых токов q = в- (у-1)

φ₃=0 – базисный узел.

φ₁G₁₁+ φ₂G₁₂=I₁₁

φ₁G₂₁+ φ₂G₂₂=I₂₂

n – число узлов.

φ₁G₁₁+ φ₂G₁₂ + …+ φ_n-1G_1(n-1) =I₁₁

φ₁G₂₁+ φ₂G₂₂ + …+ φ_n-1G_2(n-1)=I₂₂

……………………………….

φ₁G_(n-1)1+ φ₂G_(n-1)2 + …+ φ_n-1G_1(n-1) =I_(n-1)(n-1)

G_ii – собственная проводимость узла i (сумма проводимостей ветвей, сходящихся в узле i).

G_ik= G_ki – общая (взаимная) проводимость между узлами i и k (сумма проводимостей ветвей между узлами ik).

I_ii – узловой ток узла i (алгебраическая сумма токов от источников ЭДС и тока, сходящихся в узле).

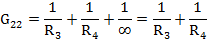
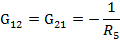
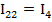
Общее решение:

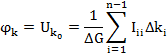
где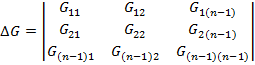

I_ii – узловой ток.

Δk_i – алгебраическое дополнение.

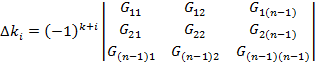
Затем через потенциалы рассчитывают токи.

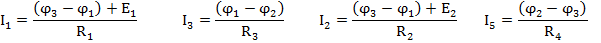
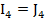
Систему уравнений можно записать в матричной форме.

(G)(φ)=(J)

Если в схеме есть идеальный источник ЭДС, целесообразно принять за базисный узел один из узлов, к которому подсоединен данный источник. Тогда потенциал 2-го узла, к которому подсоединен этот источник, будет известен и число уравнений сократится.

φ₄=0

φ₁=E₁

φ₁G₂₁+ φ₂G₂₂ + φ₃G₂₃=I₂₂

φ₁G₃₁+ φ₂G₃₂ + φ₃G₃₃=I₃₃

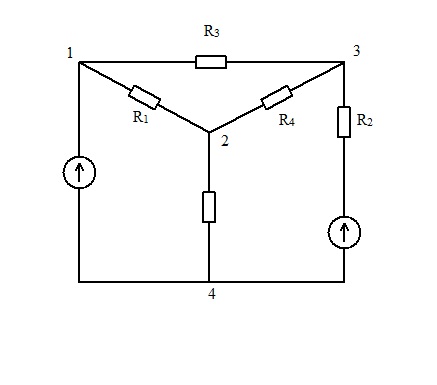
Метод двух узлов:

у=2, число уравнений – 1.

φ₂ = 0. φ₁ -?

φ₁G₁₁=I_11, где I₁₁ – алгебраическая сумма токов от источников, сходящихся в узле 1.

φ₁=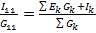

Дата добавления: 2015-08-21