Метод контурных токов.

Заключается в том, что сначала на основании уравнений по 2 Закону Кирхгофа определяют контурные токи (фиктивные токи, которые замыкаются в независимых контурах). Затем через контурные токи определяют токи в ветвях.

Число уравнений в МКТ равно числу независимых контуров (у=3). Для составления уравнений выбирают контурные токи и направляют их в одну сторону.

I₁₁R₁₁ + I₂₂R₁₂ + I₃₃R₁₃ = E₁₁

I₁₁R₂₁ + I­₂₂R₂₂ + I₃₃R₂₃ = E₂₂

I₁₁R₃₁ + I₂₂R₃₂ + I₃₃R₃₃ = E₃₃

Для n независимых контуров система составляет n уравнений.

I₁₁R₁₁ + I₂₂R₂₁ + … + I_nnR_1n = E₁₁

I₁₁R₂₁ + I­₂₂R₂₂ + … + I_nnR_2n = E₂₂

…………………………………….

I₁₁R_n1 + I₂₂R_n2 + … + I_nnR_nn = E_nn

R_ii – собственное сопротивление контура i (сумма сопротивлений, входящих в контур - всегда со знаком «+»).

R_ik=R_ki – общее или взаимное сопротивление контуров k и i (сумма сопротивлений, принадлежащих контуру i и k – всегда со знаком «-»).

E_ii – контурная ЭДС (алгебраическая сумма ЭДС, входящих в контур i).

Правила знаков:

R₁₁ = R₁ + R₄ +R₂

R₂₂ = R₂ + R₅ +R₃

R₃₃ = R₃ + R₆

R₁₂ = R₂₁ = - R₂

R₁₃ = R₃₁ = 0

R₂₃ = R₃₂ = - R₃

E₁₁ = E₁ – E₂

E₂₂ = E₂ – E₃

E₃₃ = E₃

Решая систему уравнений методом определителя:

Где ∆_R – определитель системы, элементами которого являются сопротивления.

∆_ki – алгебраические дополнения.

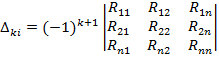
E_ii – контурная ЭДС.

∆_ki = ∆_ik

Затем через контурные токи определяем токи в ветвях. Для этого производно выбираем направление тока в ветви. Для токов, которые принадлежат одному контуру, ток равен контурному с учетом направления.

Для токов в системных ветвях ток равен разности контурных и совпадает с направлением одного из них.

I₁↑↑I₁₁ => I₁=I₁₁

I₄ = - I₂₂

I₅ = I₃₃

I₂ = I₁₁ – I₂₂

I₃ = I₂₂ – I₃₃

Систему уравнений можно записать в матричной форме.

Все источники энергии заменяются источниками ЭДС.

Если в схеме есть идеальный источник тока с R_вн = ∞, то его ток надо выбрать в качестве контурного, при этом число неизвестных контурных токов и число уравнений сокращается.

Дата добавления: 2015-08-21