Включение R, L цепи на постоянное напряжение.

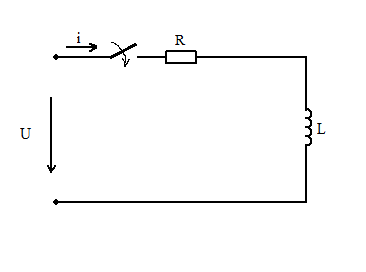Дано: U, R, L

Найти: i(t), U_R(t), U_L(t)

1) Определим начальные условия:

i_(0-) = i₍₀₊₎ = 0

2) Схема после коммутации:

U_R+U_L=U

(1)

↑Линейное дифференциальное уранение 1 порядка.

3) Решение дифференциального уравнения:

i(t)=i_пр. + i_св.

где i_пр – частное решение неоднородного уранения (1),

i_св – общее решение этого уравнения.

i_пр=?

i_св=?

(2)

ρ – корень характеристического уравнения.

- постоянная времени.

Из (2) образуем характеристическое уравнение:

R + Lρ = 0

ρ= - R/L

τ = L/R [c]

Определим постоянную интегрирования из начальных условий.

A=?

i(t)|_t=0 = 0 = => A = - U/R

, где τ = L/R

7.3.2.| Короткое замыкание R, L цепи

Дано: R, L, 0

Определить: i(t), U_R(t), U_L(t)

1) Начальные условия:

i(0_-)=i(0₊)=U/R

2) Cхема после коммутации:

U_R + U_L = 0 (По 2 закону Кирхгофа).

3) Решение дифференциального уравнения:

i(t) = i_пр + i_св

i_пр – частное решение неоднородного дифф. ур-я.

В данном случае оно однородное, i_пр=0

i_св – общее решение однородного дифф.ур-я.

R+Lρ=0 – характеристическое уравнение.

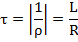
Определим А из начальных условий:

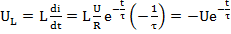
7.3.3| Включение R, L цепи на синусоидальное напряжение

Дано: R, L, U(t)=U_msin(ωt+α_u)

Определить: i(t), U_R(t), U_L(t)

1) Начальные Условия:

i(0_-)=i(0₊)=0

2) После коммутации:

U_R=U_L=U_msin(ωt+α_u)

iR+L =U_msin(ωt+α_u) (1)

Дата добавления: 2015-08-21