Изучение способов приближенного интегрирования.

Основные теоретические положения.

Постановка задачи.

Пусть необходимо вычислить определенный интеграл

(1)

Методы приближенного интегрирования основаны на использовании геометрической интерпретации значения определенного интеграла, как площади криволинейной трапеции, ограниченной осью абсцисс, прямыми x = a, x = b и кривой f (x) (рис. 1).

Для вычисления интересующей нас площади (см. рис. 1) разобьем область интегрирования на n равных частей точками:

x = a, x ₁, x ₂,..., x _i, x_{i +1},..., x _n = b.

Тогда

, (2)

где .

Значит, для вычисления интеграла (1) необходимо вычислить n площадей фигур криволинейных трапеций.

Наиболее часто при численном интегрировании используются методы прямоугольников, трапеций, Симпсона и интегрирование по методу Ромберга. Каждый из этих методов является более точным, чем предыдущий, поскольку производит аппроксимацию данных более сложной кривой.

Метод прямоугольников.

Согласно этому методу, область между точками разбиения интервала интегрирования [ a,b ] заменяется совокупностью прямоугольников, высота которых соответствует координате f(x_i) одной из точек, а ширина равна расстоянию между точками (рис. 1). Значение интеграла определяется по следующей формуле:

, (3)

где h – шаг интегрирования, определяемый из числа разбиений n интервала интегрирования [ a,b ] по формуле .

Рис. 1. Геометрическая интерпретация методов левых, правых и средних прямоугольников.

Формула (3) описывает метод левых прямоугольников, поскольку значение функции на каждом интервале интегрирования ищется по левой части этого интервала (рис. 1).

В случае использования метода правых прямоугольников значение функции находится по правой границе каждого интервала:

. (4)

Третья разновидность метода прямоугольников – метод средних прямоугольников. В нем на каждом интервале интегрирования значение функции считается в точке , а значение интеграла на всем интервале интегрирования рассчитывается по формуле

. (5)

Метод трапеций.

Согласно этому методу, каждая пара соседних точек соединяется прямой линией, образуя последовательность трапеций (рис. 2).

Рис. 2. Геометрическая интерпретация метода трапеций.

Площадь трапеции равняется полусумме оснований, умноженной на высоту, которая в данном случае равна расстоянию между точками по оси Х. Интеграл равен сумме площадей всех трапеций и находится по формуле

. (6)

Пример.

Вычислить определенный интеграл

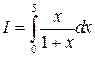
с помощью методов прямоугольников и трапеций с числом шагов, равным 5. Сравнить результаты вычислений двумя методами. (Истинное значение интеграла равно 3.208).

Метод прямоугольников.

Рассчитаем значения функции в узлах и представим результаты в виде таблицы.

xi	f (xi) слева	f (xi) справа
	0.5 0.667 0.75 0.8	0.5 0.667 0.75 0.8 0.833

По формулам (3) и (4) найдем значения интегралов методами правых и левых прямоугольников, используя постоянный шаг интегрирования 1 и соответствующие значения функции из таблицы.

Значение интеграла (слева) = 2.717, значение интеграла (справа) = 3.55.

Среднее значение интеграла равно (2.717+3.55)/2 = 3.1335.

Метод трапеций.

Аналогично методу прямоугольников начнем с составления таблицы значений функции в узлах.

xi	f (xi)
	0.5 0.667 0.75 0.8 0.833

Подставим найденные значения в формулу трапеций (6). Тогда получим:

I = 0/2+0.5+0.667+0.75+0.8+0.833/2=3.1335.

То есть, найденное с помощью метода трапеций значение интеграла, совпадает со средним значением результатов, полученных методами левых и правых прямоугольников.

Порядок выполнения работы.

Задание

Вычислить интеграл методами правых, левых прямоугольников и трапеций с числом разбиений 10 и 20. Сравнить полученные результаты.

Варианты заданий.

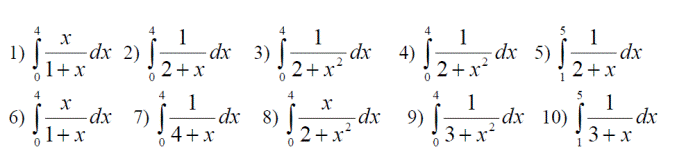
Дата добавления: 2015-10-30