Уравнения параболического типа.

К уравнениям параболического типа относятся уравнения теплопроводности или диффузии вида

где а - коэффициент теплопроводности (если u - температура) и массопереноса (если u - концентрация, давление в задачах фильтрации). Поскольку уравнение содержит производную по времени, для его решения необходимо дополнительно задавать только начальные (для t = 0), так и граничные условия (для х = 0, х = l, t> 0) (рис. 12.1).

Рисунок 12.1 – Область определения решения одномерного уравнения теплопроводности.

Уравнения гиперболического типа.

Примером уравнений гиперболического типа является волновое уравнение

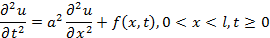
описывающее малые продольные колебания стержня и поперечные колебания струны, где u - отклонение от положения равновесия и а - скорость распространения возмущения. Волновое уравнение описывает процесс распространения малых акустических колебаний.

Уравнения эллиптического типа

Примером уравнений эллиптического типа являются уравнения Лапласа

или уравнения Пуассона

Эти уравнения описывают поток идеальной жидкости в стационарных потоках, стационарное распределение температуры или напряженности электрических или магнитных полей. Уравнение Лапласа описывает эти процессы в случае отсутствия источников энергии или стоков, а уравнение Пуассона - те же процессы при наличии распределенных в области G источников, задаваемые правой частью уравнения - f (x, y).

Поскольку уравнение Лапласа и Пуассона - стационарные, то в постановке задачи задаются только граничные условия.

Основные понятия метода сеток.

На практике решения краевых задач для уравнений с частными производными с помощью аналитических методов часто невозможно или сопряжено со значительными вычистельных трудностями. В этом случае используют приближенные численно-аналитические или численные методы. Методы этих типов являются универсальными, в отличие от чисто аналитических, и их можно применять для решения более сложных задач. Одним из таких приближенных методов является метод сеток или конечных разностей.

В методе сеток решения уравнения с частными производными, как правило, сводится к решению систем линейных алгебраических уравнений с разреженными матрицами [10]. Реализация метода осуществляется в три этапа.

1. Область непрерывного аргумента или аргументов заменяется дискретным множеством узлов, называется разностной сеткой. В ней выделяют внутренние и предельные узлы. Функция дискретного аргумента, определенная на разностной сетке, называется сеточной функцией.

2. Дифференциальное уравнение, а также начальные и граничные условия заменяются (аппроксимируются) разностными аналогами. В результате дифференциальное уравнение сводится к системе алгебраических (разностных) уравнений, которая называется разностной схемой. Такая система должна иметь единственное решение. Необходимо, чтобы с увеличением количества узлов сетки решение разностной схемы приближалось (совпадало) с решения начального дифференциального уравнения.

3. Решается система уравнений (в большинстве случаев матрица системы уравнений имеет очень большую размерность и является разреженной).

Основные идеи метода сеток рассмотрим на примере задачи Дирихле для уравнения Пуассона (12.9) с граничным условием , где g - граница области G (рис. 12.3, а), в которой ищется решение и (х, у), удовлетворяющей уравнению Пуассона и граничным условиям.

Сначала область G непрерывного изменения аргументов с границей g заменяют ее сеточной областью G, с границей g_h. Для этого проводят линии х_m = const и у_n = const, так что х_m = mh₁, m = 0,1,..., М и у_n = nh₂, n = 0,1,..., N. Величины h₁ и h₂, которые называются шагами сетки, в общем случае могут быть различными. Точки пересечения линий х_m - const и у_n = const называют узлами сетки. Различают два типа узлов - внутренние и предельные. Внутренними называют такие узлы, для которых четыре соседних узла (по два в каждом направлении) принадлежат области G + g.

Заменим дифференциальный оператор Лапласа разностным оператором. С этой целью выберем шаблон разностной схемы - система узлов, которые используются для замены производных конечными разностями. Шаблон, содержащий р точек, называется р-точечным. Для аппроксимации вторых производных, входящих в оператора Лапласа, используем пятиточечный шаблон, изображенный на рис. 12.3, б.

Используя разложение функции в ряд Тейлора на пятиточечном шаблоне, получим приближение вторых частных производных

Тогда разностное уравнение, соответствующее уравнению Пуассона можно будет записать в виде:

Тогда узловое уравнение для внутреннего узла представим в таком виде:

(12.1)

Аналогичным образом можно получить уравнения для граничных узлов. Эти уравнения могут зависеть от формы границы g.

Итак, для нахождения неизвестных значений u _m,n в узлах сетки получим систему лилинейных алгебраических уравнений, в которой число уравнений равно количеству неизвестных. Отметим, что количество уравнений может быть достаточно большим. Так, для решения задачи с высокой точностью нужно задать количество узлов М и N достаточно большим, поэтому количество уравнений может достигать нескольких тысяч. например, каждое уравнение (12.1) содержит всего пять неизвестных, но в системе их ококо N². Матрица этой системы является сильно разреженной. Существуют специализированные методы решения СЛАУ с разреженными матрицами.

Пример 12.1.

Дата добавления: 2015-10-29