Лекция 11. Визуальное моделирование динамических систем.

Поясним принцип визуального моделирования динамических систем иллюстрацией из ТАУ. В ТАУ для анализа систем управления широко используется преобразование Лапласа и специальные обозначения для отдельных типов звеньев: апериодического, интегрирующего и т.д.

Соединяя между собой звенья, выполняющие элементарные математические операции можно получить наглядное изображение динамической системы в виде структурной блок-схемы.

Предположим, что операция вычисления интеграла выполняется блоком, который изображается следующим образом:

Рисунок 11.1 – Обозначение интегратора на структурной схеме.

Рассмотрим пример составления визуальной схемы для решения дифференциального уравнения второго порядка

Пример 10.1. C оставление визуальной схемы для решения дифференциального уравнения второго порядка.

Исходное уравнение задано в виде

Преобразуем это уравнение к системе двух уравнений первого порядка, представленных в канонической форме:

Теперь для выполнения отдельных операций интегрирования воспользуемся двумя интеграторами. Для умножения отдельных переменных на числовые коэффициенты используются блоки усиления.

Блок-схемы решения отдельных уравнений и системы уравнений в целом представлены на рис. 11.2.

а) Блок-схема решения первого уравнения	б) Блок-схема решения первого уравнения
в) общая структурная схема для решения уравнения второго порядка.
Рисунок 11.2 – Формирование структурной схемы для визуального моделирования дифференциального уравнения второго порядка

Таким способом можно составлять структурные схемы для систем дифференциальных уравнений и более высоких порядков.

Следует понимать, что представление системы ОДУ в виде структурной схемы является другой формой записи собственно дифференциальных уравнений. Иногда такое представление является более удобным для восприятия. За счет наличия в библиотеке блоков большого числа стандартных компонентов иногда значительно ускоряется разработка математической модели. Такой режим программирования математической модели не требует глубокого понимания языков программирования и доступен даже новичкам.

Именно поэтому визуальное моделирование получило широчайшее распространение.

В качестве примера систем визуального моделирования в первую очередь назовем пакет Simulink программы MATLAB, программы Labview, Multisim, Electronic Workbench, Anylogic, Proteus и многие другие, менее популярные. Например, я встречал программу FluidSim – специализированный пакет для визуального моделирования гидравлических и пневматических систем.

Пример 10.2. C оставление визуальной схемы для решения системы ОДУ двигателя постоянного тока в MATLAB/Simulink.

Движение двигателя постоянного тока описывается следующей системой ОДУ второго порядка:

Структурная схема ДПТ в MATLAB/Simulink.

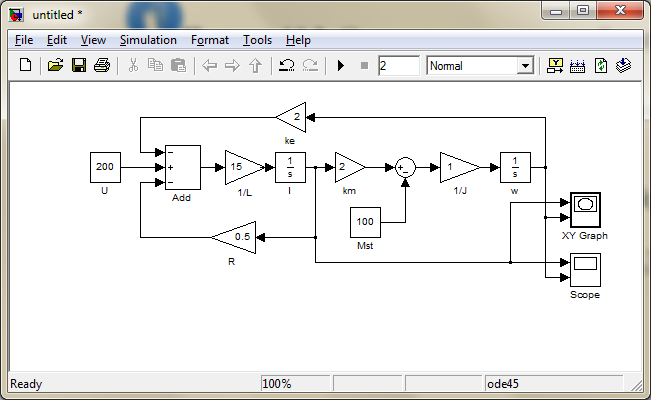
Графики запуска ДПТ во времени	Фазовый портрет процесса запуск ДПТ – w = f(I).

Дата добавления: 2015-10-29