Визуализация решений ОДУ.

При моделировании электромеханических систем в качестве аргумента функций чаще всего рассматривается время. Анализируемые уравнения описывают изменение во времени разнообразных величин: токов, мощностей, угловой скорости и пути и многое другое.

Для представления результатов решения ОДУ наиболее естественной формой являются графики зависимостей переменных от времени.

В этом очерке мы опишем пример одной динамической системы, привлекающей последние тридцать лет большое внимание исследователей. Эта трехмерная динамическая система была введена в научный обиход в 1963 году Э. Лоренцем, занимавшемся моделированием атмосферных процессов. С тех пор она вызывала и продолжает вызывать огромное число исследований и публикаций. Основной причиной, породившей такой интерес к системе уравнения Лоренца, является хаотическое поведение ее траекторий. Ясности в исследуемых вопросах еще нет. Некоторые результаты обоснованы только на "физическом уровне строгости'' или численно и говорит о сформировавшейся теории рано. Поэтому изучение рекомендуемой литературы требует довольно высокой математической подготовки. По этой же причине этот очерк не сопровождается задачами.

Система уравнений Лоренца — это трехмерная система нелинейных автономных дифференциальных уравнений первого порядка вида

В ней σ, b и r — параметры. Эта система возникла в задаче о моделировании конвективного течения жидкости, подогреваемой снизу. Такое течение описывается системой дифференциальных уравнений в частных производных

В результате численного интегрирования этой системы Э. Лоренц обнаружил, что при σ = 10, b = 8/3 и r = 28 у этой динамической системы, с одной стороны, наблюдается хаотическое, нерегулярное поведение всех траекторий (см. рис. 10.2, на котором изображена зависимость координаты y одной из траекторий от времени), а, с другой стороны, все траектории притягиваются при t →∞ к некоторому сложно устроенному множеству — аттрактору (от англ. to attract — притягивать, привлекать).

Попробуем решить систему уравнений Лоренца. Используем расширение dee программы MATLAB для быстрого задания системы уравнений.

Зачастую решения СДУ гораздо более наглядны при использовании другого типа графиков – т.н. фазовых портретов, когда независимая переменная (в нашем случае время t) рассматривается как параметр, а на графике отображается зависимость одной из переменных системы от другой переменной. Например, в курсе «Электрические машины» вы рассматривали механические характеристики АД. Зависимость угловой скорости от момента двигателя - типичный пример фазового портрета. Ведь при запуске и ток, и момент изменяются во времени.

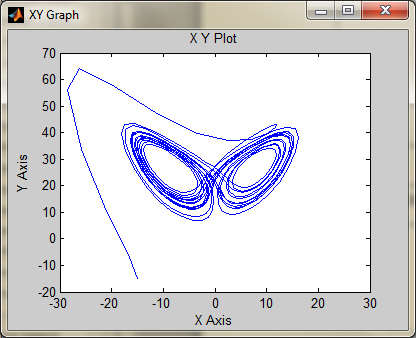
Построим фазовый портрет системы уравнений Лоренца в виде графика x = f(z). Он имеет такой вид, рис.10.3

Рисунок 10.2 – Решение уравнений Лоренца в программе MATLAB. Временные диаграммы x(t), z(t).

Рисунок 10.3 – Фазовый портрет уравнений Лоренца.

Особенностью этой фазовой траектории является то, что весь этот хаос линий не является замкнутым …

При ρ < 1 система Лоренца имеет асимптотически устойчивую в целом стационарную точку — начало координат. К ней притягиваются все траектории (см. рис. 10.4, а). Когда ρ переваливает через единицу, происходит первая бифуркация. Начало координат теряет устойчивость и от него отделяются две новые устойчивые стационарные точки, (см. рис. 10.4, б).

a) ρ = -1
a) ρ = 5 Слева x0=15 y0=-15 z0= 15 x=2.8;z=4 Справа x0=-15 y0=-15 z0=-15 x=-3.8;z=4
б) ρ = 24 Слева x0=15 y0=-15 z0= 15 Справа x0=-15 y0=-15 z0=-15
в) ρ = 28 Слева x0=15 y0=-15 z0= 15 Справа x0=-15 y0=-15 z0=-15
Рисунок 10.4 – Влияние параметра ρ на устойчивость решений уравнений Лоренца.

Дата добавления: 2015-10-29