Ферромагнетиков

Цель работы

Измерение магнитного поля и магнитной проницаемости ферромагнетика, изучение проявлений эффекта магнитного гистерезиса.

Теоретическое введение

Все вещества способны создавать магнитные поля и взаимодействовать с внешними магнитными полями. Иначе говоря, всякое вещество обладает магнитными свойствами. Это связано с тем, что по отношению к взаимодействию с магнитным полем любое вещество как макроскопическая система представляет собой скопление огромного числа микроскопических магнитных моментов.

Основной характеристикой магнитного состояния вещества как макросистемы является его намагниченность М. Если dV 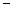физически бесконечно малый объем вещества, сохраняющий при этом его макроскопические свойства и находящийся в точке с радиус-вектором r, то произведение М (r, t) dV совпадает с усредненным суммарным значением всех микроскопических магнитных моментов, принадлежащих объему dV в момент времени t (в общем случае состояние вещества может быть неоднородным и нестационарным, что и обусловливает возможную зависимость М и от r, и от t). Так как в СИ магнитный момент измеряется в А^. м², то единицей измерения намагниченности является А/м.

Вещество, у которого всюду намагниченность М равна 0, называют ненамагниченным (или размагниченным). В противном случае говорят, что вещество намагничено. Переход из первого состояния во второе называется процессом намагничивания.

Микроскопические магнитные моменты обусловлены электронами атомов и молекул вещества. Каждый электрон, перемещаясь внутри этих мельчайших частиц вещества, во-первых, создает микроскопически малый ток, который характеризуется микроскопически малым магнитным моментом, и, во-вторых, обладает так называемым собственным магнитным моментом (им обладает покоящийся электрон и даже нейтрон, который не имеет заряда). Их происхождение сугубо квантовое.

В мельчайших частицах вещества возможны две ситуации. В одной из них, в отсутствие внешнего магнитного поля, магнитные моменты разных электронов в сумме компенсируют друг друга. Такая частица в целом магнитного момента не имеет. Атомы и молекулы этого типа называются диамагнитными, аналогично именуют и состоящие из них вещества. Иначе их называют диамагнетиками. В отсутствие внешних магнитных полей намагниченность диамагнетика равна нулю. Он ненамагничен.

Если только что упомянутой компенсации не происходит, то соответствующая мельчайшая частица вещества называется парамагнитной и парамагнитным или парамагнетиком называется вещество, состоящее из таких частиц. Из-за хаотичности теплового движения при отсутствии внешних магнитных полей магнитные моменты парамагнитных частиц ориентированы беспорядочно. Из-за этого при суммировании макроскопически большого числа этих моментов получается нуль. Следовательно, и в этом случае намагниченность равна нулю, т.е. парамагнетик размагничен.

Наконец, существует класс твердых сред, разительно отличающихся от диа- и парамагнитных материалов. Из таких сред наиболее распространенным является железо. Поэтому их стали называть ферромагнитными или ферромагнетиками. В них и при отсутствии внешних магнитных полей существуют участки макроскопических размеров, в которых суммы всех входящих в них микроскопических моментов не равны нулю. Это связано с особенностями атомно-молекулярных взаимодействий в таких средах, из-за чего разным микроскопическим моментам, образующих макросистему, энергетически не выгодно ориентироваться беспорядочно (как, например, в парамагнетиках). Они выстроены преимущественно в одном каком-то порядке. Такие области в веществе называются магнитными доменами. В них самопроизвольно или спонтанно существует ненулевая намагниченность. Часто количества ферромагнитного вещества оказывается достаточно много в том смысле, что в таком веществе формируется много доменов с разными ориентациями их намагниченностей. Тогда суммарный магнитный момент всего объема вещества снова оказывается нулевым. В этом случае в целом ферромагнетик размагничен несмотря на то, что в пределах каждого домена это не так.

Теперь о механизмах намагничивания разных типов магнетиков.

Намагничивание диамагнетиков происходит при включении внешнего магнитного поля. Включение поля хотя и происходит обычно достаточно быстро, но все же занимает некоторое время, в течение которого поле изменяется от нулевого значения до некоторого значения В ¹ 0.

Вспомним теперь об одном важном электромагнитном явлении: в каждом переменном во времени магнитном поле всегда возникает электрическое поле. Этот эффект называется электромагнитной индукцией. Поэтому при включении магнитного поля электроны диамагнетика оказываются подверженными действию индукционного электрического поля. Оно вызывает небольшие искажения электронных токов, которые можно трактовать как прибавление к первоначальным токам дополнительных индукционных, из-за которых расстраивается первоначальная взаимная компенсация электронных магнитных моментов. В результате у мельчайших частиц диамагнитного вещества возникает наведенный включением поля магнитный момент. Теперь вспомним об общем свойстве индукционных токов: они всегда имеют такое направление, что их магнитные поля ослабляют действие причины, возбуждающей этот ток (правило Ленца). Эта особенность индукционных токов в диамагнетике проявляется в том, что он отталкивается от источника внешнего поля, т.е. стремится выйти из этого поля. Эффект диамагнитного отталкивания слабый. Это объясняется малостью индукционно наведенной намагниченности, появляющейся вследствие раскомпенсации электронных магнитных моментов в диамагнитных частицах. При этом она оказывается ориентированной против внешнего поля.

Агрегатное состояние диамагнетиков бывает различным: cущест-вуют диамагнитные газы, жидкости и твердые тела. Характерной особенностью диамагнитной намагниченности является ее независимость от температуры.

Механизм намагничивания парамагнетиков ориентационный. Любой магнитный момент, попав во внешнее поле, стремится сориентироваться вдоль поля. Этим исключается первоначальная хаотичность направлений магнитных моментов мельчайших частиц парамагнитной среды. В результате суммирование большого числа таких моментов уже не приводит к нулю. Поэтому возникает намагниченность, ориентированная вдоль поля. При такой ее ориентации взаимодействие внешнего поля с намагниченным парамагнетиком сводится к их притяжению: намагниченный парамагнетик втягивается во внешнее поле.

Подобно диамагнетикам парамагнетики также бывают в разных агрегатных состояниях, но отличаются от них существенной зависимостью парамагнитной намагниченности от температуры.

Намагничивание ферромагнетика сходно с предыдущим случаем в том отношении, что оно также имеет ориентационный характер. Но есть и принципиальное отличие, состоящее в том, что в ферромагнетике поле разворачивает не отдельные микроскопические магнитные моменты, а намагниченности отдельных доменов, которые стремятся сориентироваться вдоль поля. Поэтому в одном и том же внешнем поле намагниченность любого ферромагнетика гораздо больше намагниченности любой парамагнитной среды. Еще одно существенное отличие состоит в том, что после выключения внешнего поля намагниченность парамагнетика также исчезает. Этого не происходит в случае ферромагнетиков. Дело в том, что каждый домен является макросистемой, находящейся в твердом состоянии. Поэтому восстановление беспорядка в ориентации доменов сильно затруд-

нено. Соответственно, после выключения внешнего намагничивающего поля ферромагнетик остается намагниченным. Именно из таких ферромагнитных материалов изготавливаются так называемые постоянные магниты. Еще одним важным свойством ферромагнитной намагниченности является ее существенная зависимость от температуры. При этом существует такая температура, называемая точкой Кюри, при превышении который ферромагнитный порядок разрушается и ферромагнетик превращается в парамагнетик.

Наконец, приведем данные об относительной иерархии абсолютных значений намагниченностей разных типов магнетиков при одном и том же намагничивающем поле и температуре (ниже точки Кюри ферромагнетика): парамагнитная намагниченность на два–три порядка больше диамагнитной, а ферромагнитная намагниченность на шесть–семь порядков превышает парамагнитную.

Напомним, что намагниченность имеет смысл магнитного момента единицы объема магнетика. Это означает, что в намагниченном магнетике циркулируют токи, обусловленные именно его намагниченным состоянием и характеризуемые этим магнитным моментом. Эти токи называются токами намагничивания. В этом случае магнитное поле В в магнетике уже не определяется одними только внешними токами. В этом случае это поле является суперпозицией поля В ₀, порождаемого этими токами в вакууме, и поля В ₁, создаваемого токами намагничивания:

В = В ₀ + В ₁. (1)

Оказывается, что эта формула может быть преобразована так:

B = m ₀ (H + M). (2)

В (2) m ₀ – магнитная постоянная (равна 4p×10^-7 Гн/м), М – намагниченность, величина H называется напряженностью магнитного поля (в СИ измеряется в A/м). В стационарном случае напряженность магнитного поля зависит только от внешних токов. Это является следствием одного из фундаментальных законов стационарного магнетизма, который выражается соотношением

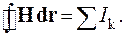(3)

Левая часть (3) является циркуляцией Н по любому замкнутому контуру L. Правая часть равна сумме внешних токов, пронизывающих контур L. В частности, если внешний ток протекает по одному неразветвленному проводу, то из (3) следует, что напряженность магнитного поля пропорциональна силе тока в этом проводе.

В изотропных средах (их свойства одинаковы по различным направлениям) векторы В и Н, помимо (2), связаны также соотношением

В = m₀m Н. (4)

Коэффициент m безразмерен, характеризует магнитные свойства среды и называется ее магнитной проницаемостью.

Сравнивая (1) и (2), видим, что произведение m ₀ Н является магнитной индукцией, которая при заданных внешних токах возникала бы не в веществе, а в вакууме. Следовательно, магнитная проницаемость показывает, насколько магнитное поле в веществе отличается от соответствующего поля в вакууме.

Магнитная проницаемость диамагнетиков постоянна и чуть меньше единицы. Это как раз и означает, что магнитное поле токов намагничивания диамагнетика направлено против внешнего магнитного поля и незначительно его ослабляет.

Магнитная проницаемость парамагнетиков при фиксированной температуре постоянна и несколько больше единицы, в чем выражается одинаковая направленность магнитного поля токов намагничивания парамагнетика и внешнего поля. Таким образом, это поле усиливает в не очень сильной степени действие внешнего магнитного поля.

Магнитная проницаемость ферромагнетиков имеет ряд важных особенностей. Во-первых, она гораздо больше единицы, по порядку величины достигает значений до 10⁶. Во-вторых, магнитная проницаемость ферромагнитных сред не является постоянной величиной. Она зависит от напряженности магнитного поля. Эта зависимость неоднозначна, что связано с явлением остаточного намагничивания. Остановимся подробнее на последнем, его иллюстрирует рис 1.

Допустим, что внешний ток, вызывающий намагничивание ферромагнетика, постепенно возрастает от нуля до некоторого достаточно большого значения (1-ый этап намагничивания). После этого, не изменяя своего направления, ток уменьшается до нуля, затем изменяет свое направление на противоположное, достигает по абсолютной величине значения, которое он имел в конце 1-го этапа (2-ой этап процесса). Затем ток снова возрастает, сохраняя ранее измененное направление, уменьшается по абсолютной величине, проходит через нулевое значение, второй раз изменяет свое направление на обратное предыдущему и повторно возвращается к значению, достигнутому в конце 1-го этапа (3-ий этап процесса). При охарактеризованных изменениях векторная природа индукции и напряженности магнитного поля проявляется в том, что эти величины принимают как положительные, так и отрицательные значения. Поэтому ниже эти величины будут записываться без выделения их жирным шрифтом, а как обычные алгебраические величины, т.е. будут обозначаться, соответственно, через В и Н.

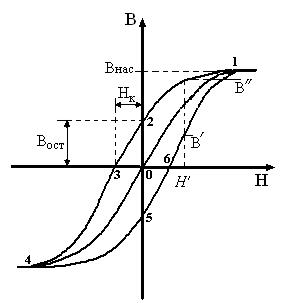
Рис 1.

На 1-ом этапе графиком зависимости В (Н) является линия, начинающаяся в начале координат и заканчивающаяся в точке 1 на рис. 1 (эта линия называется нулевой кривой намагничивания ферромагнетика). Она близка к прямой только вблизи начала координат, т.е. величину m можно считать примерно постоянной только в этой области. С увеличением Н величина m становится зависящей от Н. При достаточно больших Н нулевая кривая намагничивания практически превращается в горизонтальную прямую. Возникает состояние так называемого магнитного насыщения ферромагнетика. В этом состоянии намагниченность ферромагнетика достигает максимального значения, что обусловлено выстраиванием намагниченностей всех его доменов в одном направлении. После этого с дальнейшим ростом Н намагниченность не изменяется (рис. 1).

На 2-ом этапе процесса оказывается, что зависимость В (Н) отличается от имевшей место на нулевой кривой намагниченности: индукция магнитного поля будет уменьшаться по кривой 1-2, расположенной левее нулевой кривой. Видно, что, по крайней мере, в начале 2-го этапа величина В изменяется медленнее, чем в конце первого. Соответственно, в этой области магнитная проницаемость m (Н) на 2-ом этапе больше аналогичной величины на 1-ом этапе. Это означает, что магнитная проницаемость ферромагнетика не является однозначной функцией Н: ее вид определяется также предысторией изменения магнитного состояния ферромагнетика. Физическая причина такого явления обусловлена затрудненностью разориентации магнитных доменов из-за того, что они являются твердотельными макросистемами. Значению Н = 0 (оно реализуется при нулевом внешнем токе) на жирной кривой соответствует В ¹ 0. Это значение называется остаточной индукцией и на рис. 1 обозначено через В _ост. Существование В _ост ¹ 0 означает, что при выключении внешних намагничивающих токов в рассматриваемом процессе ферромагнетик остается намагниченным, превращаясь в постоянный магнит.

Чтобы его размагнитить, нужно по оси Н уйти левее начала координат, т.е. поменять направление протекания намагничивающего тока. При этом магнитное состояние ферромагнетика будет изменяться в соответствии с нижней частью жирной кривой. В этой области при 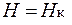магнитная индукция В обращается в нуль, т.е. ферромагнетик размагничивается. Величина Н _к называется коэрцитивной силой ранее сформировавшегося постоянного магнита. Только при 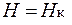удается восстановить разупорядоченность разных доменов ферромагнетика.

Если далее двигаться по оси Н влево до значения, при котором достигается «левое» насыщение (конец второго этапа) и затем вновь вернуться к значению «правого» насыщения, т.е. перейти к 3–ему этапу процесса, то график зависимости В (Н) замкнется третьей кривой 4-5-6-1 на рис. 1. В целом фигура, изображенная на рис. 1, называется петлей магнитного гистерезиса ферромагнетика. Она является предметом изучения в данной лабораторной работе.

Для дальнейшего существенны два замечания. Рассмотрим рис. 2. На нем схематично изображен образец ферромагнетика с намотанными на него двумя токопроводящими обмотками 1 и 2. Напряжение на обмотке (1) пропорционально Н, создаваемой током в (1). Напряжение на обмотке (2) пропорционально В. Обоснования этих замечаний для данной работы несущественны. Поэтому они не приводятся.

намагничи- образец измеритель-

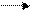вающая ная

Дата добавления: 2015-10-29