
Читайте также:
|
Генеральною сукупністю називається множина однотипних об’єктів, кількісна чи якісна ознака яких підлягає вивченню. Підмножина об’єктів, дібраних відповідним способом із генеральної сукупності, називається вибірковою сукупністю.
Нехай із генеральної сукупності отримано вибірку, причому значення  спостерігалося
спостерігалося  разів,
разів, 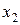 –
–  разів і т. д.,
разів і т. д.,  – обсяг вибірки. Значення, що спостерігаються, називаються варіантами, а послідовність варіант, записаних у порядку зростання, – варіаційним рядом. Кількість спостережень називається частотами, а їх відношення до обсягу вибірки – відносними частотами.
– обсяг вибірки. Значення, що спостерігаються, називаються варіантами, а послідовність варіант, записаних у порядку зростання, – варіаційним рядом. Кількість спостережень називається частотами, а їх відношення до обсягу вибірки – відносними частотами.
Статистичним розподілом вибірки називається перелік варіант і відповідних їм частот або відносних частот. Також можна задати його у вигляді послідовності інтервалів і відповідних їм частот.
Емпіричною функцією розподілу називають функцію 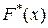 , що визначає для кожного значення
, що визначає для кожного значення 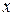 відносну частоту події
відносну частоту події  :
:
 ,
,
де 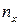 – кількість спостережень, при яких спостерігалося значення ознаки, менше за
– кількість спостережень, при яких спостерігалося значення ознаки, менше за 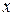 ;
;  – обсяг вибірки.
– обсяг вибірки.
Функцію розподілу 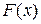 генеральної сукупності називають теоретичною функцією розподілу. Для наочності будують різні графіки статистичного розподілу.
генеральної сукупності називають теоретичною функцією розподілу. Для наочності будують різні графіки статистичного розподілу.
Полігоном частот називають ламану, відрізки якої з’єднують точки  . Аналогічно будують полігон відносних частот.
. Аналогічно будують полігон відносних частот.
У випадку неперервної ознаки доцільно будувати гістограму. Гістограмою частот називають фігуру, що складається з прямокутників, основами яких є часткові інтервали довжиною  , а висоти рівні відношенню
, а висоти рівні відношенню  (щільність частоти). Площа гістограми частот дорівнює обсягу вибірки.
(щільність частоти). Площа гістограми частот дорівнює обсягу вибірки.
Нехай 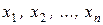 – дані спостережень за випадковою величиною Х.
– дані спостережень за випадковою величиною Х.
Вибіркова середня 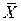 обчислюється за формулами:
обчислюється за формулами:
а) якщо дані не згруповані, то 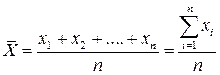 ;
;
б) якщо дані згруповані, то  .
.
Вибіркова дисперсія 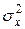 обчислюється за формулами:
обчислюється за формулами:
а) якщо дані не згруповані, то 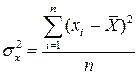 ;
;
б) якщо дані згруповані, то  .
.
Дата добавления: 2015-10-28; просмотров: 103 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Випадкових величин | | | ЗАВДАННЯ КОНТРОЛЬНОЇ РОБОТИ |