Основні поняття. Визначення ймовірності

КОЛЕДЖ

КЛАСИЧНИЙ ПРИВАТНИЙ УНІВЕРСИТЕТ

ТЕОРІЯ ЙМОВІРНОСТЕЙ

ТА МАТЕМАТИЧНА СТАТИСТИКА

Методичні матеріали та вказівки

до виконання контрольних робіт

для студентів заочної форми навчання

Енергодар

ЗМІСТ

ВСТУП 4

1. ВИПАДКОВІ ПОДІЇ 5

1.1. Основні поняття. Визначення ймовірності 5

1.2. Елементи комбінаторики 6

1.3. Теореми додавання та множення ймовірностей 6

1.4. Формула повної ймовірності і формула Байєса 7

1.5. Схема випробувань із повтореннями 8

2. ВИПАДКОВІ ВЕЛИЧИНИ 10

2.1. Закони розподілу і числові характеристики

випадкових величин 10

2.2. Нормальний закон розподілу 11

3. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ 13

3.1. Первинна обробка і графічне подання вибіркових даних. Числові характеристики вибіркової сукупності 13

3.2. Елементи теорії кореляції 14

4. ЗАВДАННЯ КОНТРОЛЬНОЇ РОБОТИ 17

5. ЗРАЗОК РОЗВ’ЯЗАННЯ НУЛЬОВОГО ВАРІАНТА 31

6. ПЕРЕЛІК ПИТАНЬ З ДИСЦИПЛІНИ 46

ЛІТЕРАТУРА 49

ДОДАТКИ 50

ВСТУП

Теорія ймовірностей і математична статистика – одна з важливих математичних дисциплін, які вивчають студенти заочної форми навчання. У процесі вивчення дисципліни розглядаються закономірності розвитку окремого випадкового явища та масових випадкових явищ, прогнозування їх характеристик, кількісні та якісні методи аналізу цих закономірностей.

Основною формою навчання студента-заочника є самостійна робота над навчальним матеріалом, що включає читання підручників, розв’язання задач, виконання контрольних завдань. Пропонований посібник охоплює теми усіх практичних занять, передбачених навчальним планом.

Контрольна робота має складатися з таких частин:

1) титульного аркуша;

2) основної частини, що включає умову задачі та її розв’язок (докладно викладений, із відповідними посиланнями на теоретичні питання й вказівками необхідних формул).

Під час екзаменаційної сесії студент повинен пройти співбесіду по зарахованій контрольній роботі. Студент виконує той варіант контрольної роботи, номер якого збігається з номером його прізвища у списку в журналі академічної групи.

До заліку (іспиту) з дисципліни допускаються студенти, що виконали контрольну роботу в повному обсязі.

1. ВИПАДКОВІ ПОДІЇ

Основні поняття. Визначення ймовірності

Випробування – реальний або уявний експеримент (виконуваний за певної незмінної сукупності умов), за результатами якого спостерігають.

Подія – результат випробування.

Деяка подія, що неодмінно відбудеться в результаті випробування називається достовірною. Подія, яка в даному випробуванні не може відбутись, називається неможливою.

Подіяназивається випадковою, якщо вона може відбутися або не відбутися. Події позначаються літерами .

Подія, що знаходиться поза настанням події , називається протилежною і позначається як .

Імовірністю випадкової події називається об'єктивна числова міра появи цієї події. Імовірність випадкової події дорівнює відношенню кількості сприятливих випадків до кількості усіх можливих взаємовиключальних і рівноможливих випадків випробування й обчислюється за формулою:

(1.1)

Властивості ймовірності:

1) імовірність достовірної події дорівнює 1;

2) імовірність неможливої події дорівнює 0;

3) імовірність випадкової події є додатним числом, що міститься між 0 та 1.

Статистичною ймовірністю події називається відношення кількості випробувань, у яких подія відбулась, до загальної кількості виконаних випробувань :

. (1.2)

1.2. Елементи комбінаторики

Перестановками називаються комбінації, що складаються з одних і тих самих елементів і відрізняються тільки порядком їх розташування. Кількість усіх можливих перестановок

. (1.3)

Розміщеннями називають комбінації, що складаються з різних елементів по елементів, які відрізняються або їх складом, або порядком. Кількість усіх можливих розміщень

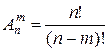. (1.4)

Сполученнями називають комбінації, складені з різних елементів по елементів, що відрізняються хоча б одним елементом. Кількість усіх можливих сполучень

. (1.5)

Дата добавления: 2015-10-28