
Читайте также:
|
Завдання №1
1. У майстерню на ремонт надійшло 15 телевізорів. Відомо, що 6 із них потребують загального регулювання. Майстер бере п’ять телевізорів навмання. Яка ймовірність того, що два з них мають потребу в загальному регулюванні?
2. З колоди карт (36 шт.) одночасно витягають 3 карти. Яка ймовірність того, що це будуть карти: а) однієї масті; б) одного кольору?
3. Серед 20 однакових за зовнішнім виглядом зошитів 16 – у клітинку. Узято 4 зошити. Знайти ймовірність того, що 2 з них – зошити в клітинку.
4. Кинуто три монети. Знайти ймовірність того, що випадуть два «орли».
5. З урни, що містить чотири білих і п’ять чорних куль, навмання виймають дві кулі. Знайти ймовірність того, що одна з них – біла, а інша – чорна.
6. У магазині працюють 10 продавців, 6 із них – жінки. У зміну зайняті 3 продавці. Знайти ймовірність того, що у випадково вибрану зміну вийдуть двоє чоловіків і одна жінка.
7. Серед 25 однакових за зовнішнім виглядом зошитів 15 – у клітинку. Узято 5 зошитів. Знайти ймовірність того, що 3 з них – зошити в клітинку.
8. У майстерню на ремонт надійшло 12 телевізорів. Відомо, що 5 із них потребують загального регулювання. Майстер бере чотири телевізора навмання. Яка ймовірність того, що два з них мають потребу в загальному регулюванні?
9. З урни, що містить чотири білих і шість чорних куль, навмання виймають дві кулі. Знайти ймовірність того, що одна з них – біла, а інша – чорна.
10. З колоди карт (36 шт.) одночасно витягають 5 карт. Яка ймовірність того, що це будуть карти: а) однієї масті; б) одного кольору?
Завдання №2
1. Податкова інспекція проводе перевірку документації трьох фірм. Ймовірність того, що при перевірці будуть виявлені порушення для першої фірми дорівнює 0,2, для другої та третьої – 0,1, відповідно. Знайти ймовірність того, що порушення будуть виявлені: а) тільки на одній якій-небудь фірмі; б) тільки на двох фірмах; в) на трьох фірмах.
2. Проводиться хімічний аналіз проб води з трьох джерел. Ймовірність того, що хімічний склад води з першого джерела знаходиться в границях норми, дорівнює 0,7; з другого – 0,9; з третього – 0,8. Знайти ймовірність того, що в границях норми буде вода: а) з усіх трьох джерел; б) тільки з двох яких-небудь джерел; в) хоча б з одного джерела.
3. Три студента складають іспит. Для першого студента ймовірність скласти іспит дорівнює 0,9, для другого – 0,8, для третього – 0,7. Знайти ймовірність того, що: а) іспит складуть всі студенти; б) іспит складе тільки один студент; в) іспит складе хоча б один студент.
4. У цеху 3 верстати. Ймовірність відмови І-го дорівнює 0,1; ІІ-го – 0,2;
ІІІ-го – 0,1. Обчислити ймовірність роботи: а) всіх верстатів; б) двох верстатів; в) хоча б одного верстата.
5. Податкова інспекція проводе перевірку документації трьох фірм. Ймовірність того, що при перевірці будуть виявлені порушення для першої фірми дорівнює 0,1, для другої та третьої – 0,2, відповідно. Знайти ймовірність того, що порушення будуть виявлені: а) тільки на одній якій-небудь фірмі; б) тільки на двох фірмах; в) на трьох фірмах
6. Проводиться хімічний аналіз проб води з трьох джерел. Ймовірність того, що хімічний склад води з першого джерела знаходиться в границях норми, дорівнює 0,8; з другого – 0,7; з третього – 0,9. Знайти ймовірність того, що в границях норми буде вода: а) з усіх трьох джерел; б) тільки з двох яких-небудь джерел; в) хоча б з одного джерела.
7. Три студента складають іспит. Для першого студента ймовірність скласти іспит дорівнює 0,8, для другого – 0,9, для третього – 0,7. Знайти ймовірність того, що: а) іспит складуть всі студенти; б) іспит складе тільки один студент; в) іспит складе хоча б один студент.
8. У цеху 3 верстати. Ймовірність відмови І-го дорівнює 0,2; ІІ-го – 0,1;
ІІІ-го – 0,3. Обчислити ймовірність роботи: а) всіх верстатів; б) двох верстатів; в) хоча б одного верстата.
9. Податкова інспекція проводе перевірку документації трьох фірм. Ймовірність того, що при перевірці будуть виявлені порушення для першої фірми дорівнює 0,1, для другої та третьої – 0,2, відповідно. Знайти ймовірність того, що порушення будуть виявлені: а) тільки на одній якій-небудь фірмі; б) тільки на трьох фірмах; в) хоча б на одній фірмі.
10. Проводиться хімічний аналіз проб води з трьох джерел. Ймовірність того, що хімічний склад води з першого джерела знаходиться в границях норми, дорівнює 0,8; з другого – 0,6; з третього – 0,9. Знайти ймовірність того, що в границях норми буде вода: а) з усіх трьох джерел; б) тільки з одного джерела; в) хоча б з одного джерела.
Завдання №3
Використовуючи локальну й інтегральну теореми Муавра–Лапласа, знайти ймовірності зазначеної події.
У кожному з  незалежних випробувань подія
незалежних випробувань подія  відбувається з постійною ймовірністю
відбувається з постійною ймовірністю  . Знайти ймовірність того, що подія
. Знайти ймовірність того, що подія  відбувається:
відбувається:
а) точно  разів; б) не менше ніж
разів; б) не менше ніж  і не більше ніж
і не більше ніж  разів.
разів.
| Завдання | 
| 
| 
| 
|
| 0,35 | ||||
| 0,38 | ||||
| 0,41 | ||||
| 0,44 | ||||
| 0,47 | ||||
| 0,50 | ||||
| 0,53 | ||||
| 0,57 | ||||
| 0,60 | ||||
| 0,63 |
Завдання №4
Задано закон розподілу дискретної випадкової величини  (у першому рядку зазначено можливі значення величини
(у першому рядку зазначено можливі значення величини  , у другому – подано ймовірності
, у другому – подано ймовірності  цих значень). Знайти: математичне сподівання
цих значень). Знайти: математичне сподівання  ; дисперсію
; дисперсію  ; середнє квадратичне відхилення
; середнє квадратичне відхилення  .
.
1.
| Х1 | |||||
| Р1 | 0,05 | 0,18 | 0,23 | 0,41 | 0,13 |
2.
| Х1 | |||||
| Р1 | 0,15 | 0,08 | 0,35 | 0,31 | 0,11 |
3.
| Х1 | -1 | ||||
| Р1 | 0,12 | 0,17 | 0,18 | 0,38 | 0,15 |
4.
| Х1 | |||||
| Р1 | 0,35 | 0,21 | 0,18 | 0,14 | 0,12 |
5.
| Х1 | |||||
| Р1 | 0,15 | 0,18 | 0,22 | 0,25 | 0,20 |
6.
| Х1 | -2 | ||||
| Р1 | 0,18 | 0,23 | 0,21 | 0,17 | 0,21 |
7.
| Х1 | -1 | ||||
| Р1 | 0,12 | 0,17 | 0,18 | 0,38 | 0,15 |
8.
| Х1 | |||||
| Р1 | 0,35 | 0,21 | 0,18 | 0,14 | 0,12 |
9.
| Х1 | |||||
| Р1 | 0,15 | 0,18 | 0,22 | 0,25 | 0,20 |
10.
| Х1 | -2 | ||||
| Р1 | 0,18 | 0,23 | 0,21 | 0,17 | 0,21 |
Завдання №5
Оцінювання відхилення відносної частоти від постійної ймовірності в незалежних випробуваннях.
У кожному з  незалежних випробувань подія
незалежних випробувань подія 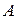 відбувається з постійною ймовірністю
відбувається з постійною ймовірністю 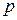 . Знайти ймовірність того, що відносна частота
. Знайти ймовірність того, що відносна частота  цієї події відрізняється за абсолютною величиною від імовірності
цієї події відрізняється за абсолютною величиною від імовірності 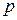 не більше ніж на
не більше ніж на  .
.
| Завдання | 
| 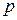
| 
|
| 0,84 | 0,054 | ||
| 0,83 | 0,053 | ||
| 0,82 | 0,052 | ||
| 0,81 | 0,051 | ||
| 0,8 | 0,05 | ||
| 0,79 | 0,049 | ||
| 0,78 | 0,048 | ||
| 0,77 | 0,047 | ||
| 0,76 | 0,046 | ||
| 0,75 | 0,045 |
Завдання №6
Для безперервної випадкової величини  , щільність розподілу ймовірностей якої відповідає нормальному закону, задані математичне сподівання
, щільність розподілу ймовірностей якої відповідає нормальному закону, задані математичне сподівання  й середнє квадратичне відхилення
й середнє квадратичне відхилення 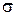 . Знайти ймовірність того, що: 1) випадкова величина
. Знайти ймовірність того, що: 1) випадкова величина  набуде значення в заданому інтервалі
набуде значення в заданому інтервалі  ; 2) абсолютна величина відхилення випадкової величини від її математичного сподівання не перевищує
; 2) абсолютна величина відхилення випадкової величини від її математичного сподівання не перевищує  .
.
1.  = 12;
= 12; 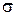 = 5;
= 5;  8;
8;  18;
18;  = 10.
= 10.
2.  = 7;
= 7; 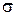 = 3;
= 3;  3;
3;  13;
13;  = 6.
= 6.
3.  = 15;
= 15; 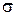 = 5;
= 5;  11;
11;  21;
21;  = 6.
= 6.
4.  = 8;
= 8; 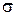 = 2;
= 2;  4;
4;  14;
14;  = 6.
= 6.
5.  = 13;
= 13; 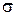 = 3;
= 3;  9;
9;  19;
19;  = 4.
= 4.
6.  = 10;
= 10; 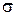 = 4;
= 4;  8;
8;  20;
20;  = 8.
= 8.
7.  = 14;
= 14; 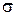 = 4;
= 4;  10;
10;  20;
20;  = 10.
= 10.
88.  = 9;
= 9; 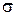 = 5;
= 5;  5;
5;  15;
15;  = 8.
= 8.
9.  = 11;
= 11; 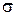 = 3;
= 3;  7;
7;  17;
17;  = 10.
= 10.
10.  = 10;
= 10; 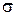 = 4;
= 4;  6;
6;  16;
16;  = 10.
= 10.
Завдання №7
Подано варіаційний ряд випадкових чисел із зазначенням інтервалів і частот. Необхідно: 1) знайти середнє арифметичне  ; 2) визначити дисперсію
; 2) визначити дисперсію  і середньоквадратичне відхилення
і середньоквадратичне відхилення 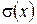 ; 3) побудувати гістограму частот; 4) за допомогою критерію Пірсона перевірити гіпотезу про нормальний розподіл вибірки.
; 3) побудувати гістограму частот; 4) за допомогою критерію Пірсона перевірити гіпотезу про нормальний розподіл вибірки.
| Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi |
| 1-3 | 2-6 | 0-4 | 10-20 | 7-9 | |||||
| 3-5 | 6-10 | 4-8 | 20-30 | 9-11 | |||||
| 5-7 | 10-14 | 8-12 | 30-40 | 11-13 | |||||
| 7-9 | 14-18 | 12-16 | 40-50 | 13-15 | |||||
| 9-11 | 18-22 | 16-20 | 50-60 | 15-17 | |||||
| 11-13 | 22-26 | 20-24 | 60-70 | 17-19 | |||||
| 13-15 | 26-30 | 24-28 | 70-80 | 19-21 | |||||
| 15-17 | 30-34 | 28-32 | 80-90 | 21-23 | |||||
| 17-19 | 34-38 | 32-36 | 90-100 | 23-25 | |||||
| 19-21 | 38-42 | 36-40 | 100-110 | 25-27 | |||||
| 21-23 | 42-46 | 40-44 | 110-120 | 27-29 | |||||
| 23-25 | 46-50 | 44-48 | 120-130 | 29-31 | |||||
| 25-27 | 50-54 | 48-52 | 130-140 | 31-33 | |||||
| 27-29 | 54-58 | 52-56 | 140-150 | 33-35 | |||||
| 29-31 | 58-62 | 56-60 | 150-160 | 35-37 | |||||
| 31-33 | 62-66 | 60-64 | 160-170 | 37-39 | |||||
| 33-35 | 66-70 | 64-68 | 170-180 | 39-41 | |||||
| 35-37 | 70-74 | 68-72 | 180-190 | 41-43 | |||||
| 37-39 | 74-78 | 72-76 | 190-200 | 43-45 | |||||
| 39-41 | 78-82 | 76-80 | 200-210 | 45-47 |
| Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi | Інтервали (ai,bi) | Частота mi |
| 402-405 | 105-110 | 110-120 | 12-13 | 10-16 | |||||
| 405-408 | 110-115 | 120-130 | 13-14 | 16-22 | |||||
| 408-411 | 115-120 | 130-140 | 14-15 | 22-28 | |||||
| 411-414 | 120-125 | 140-150 | 15-16 | 28-34 | |||||
| 414-417 | 125-130 | 150-160 | 16-17 | 34-40 | |||||
| 417-420 | 130-135 | 160-170 | 17-18 | 40-46 | |||||
| 420-423 | 135-140 | 170-180 | 18-19 | 46-52 | |||||
| 423-426 | 140-145 | 180-190 | 19-20 | 52-58 | |||||
| 426-429 | 145-150 | 190-200 | 20-21 | 58-64 | |||||
| 429-432 | 150-155 | 200-210 | 21-22 | 64-70 | |||||
| 432-435 | 155-160 | 210-220 | 22-23 | 70-76 | |||||
| 435-438 | 160-165 | 220-230 | 23-24 | 76-82 | |||||
| 438-441 | 165-170 | 230-240 | 24-25 | 82-88 | |||||
| 441-444 | 170-175 | 240-250 | 25-26 | 88-94 | |||||
| 444-447 | 175-180 | 250-260 | 26-27 | 94-100 | |||||
| 447-450 | 180-185 | 260-270 | 27-28 | 100-106 | |||||
| 450-453 | 185-190 | 270-280 | 28-29 | 106-112 | |||||
| 453-456 | 190-195 | 280-290 | 29-30 | 112-118 | |||||
| 456-459 | 195-200 | 290-300 | 30-31 | 118-124 | |||||
| 459-462 | 200-205 | 300-310 | 31-32 | 124-130 |
Дата добавления: 2015-10-28; просмотров: 141 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Первинна обробка і графічне подання вибіркових даних. Числові характеристики вибіркової сукупності | | | ЗРАЗОК РОЗВ’ЯЗАННЯ НУЛЬОВОГО ВАРІАНТА |