Випадкових величин

Випадковою називається величина, яка може набувати різних числових значень. Дискретною називається випадкова величина, що має скінченну множину значень.

Співвідношення між значеннями випадкової величини та їх імовірностями називається законом розподілу випадкової величини.

Закон розподілу дискретної випадкової величини (ДВВ) можна задавати у вигляді таблиці:

			...
			...

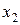
де .

Математичним сподіванням ДВВ називається сума добутків усіх її значень на відповідні їм імовірності:

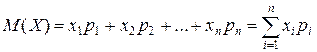. (2.1)

Дисперсія ДВВ – це математичне сподівання квадрата відхилення випадкової величини від її математичного сподівання:

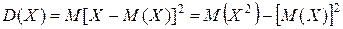. (2.2)

Середнім квадратичним відхиленням випадкової величини називається арифметичне значення квадратного кореня від дисперсії:

. (2.3)

Універсальним способом задання закону розподілу ймовірностей є функція розподілу 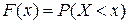, яка виражає ймовірність того, що випадкова величина набуде якого-небудь значення, менше від заданого.

Щільністю ймовірності називається похідна від функції розподілу випадкової величини .

Математичне сподівання неперервної випадкової величини:

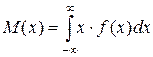або 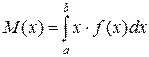. (2.4)

Дисперсія неперервної випадкової величини:

(2.5)

або

. (2.5а)

Нормальний закон розподілу

Нормальний закон розподілу задається щільністю

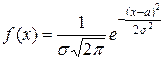. (2.6)

Параметри і , які входять до виразу щільності розподілу, є відповідно математичним сподіванням та середнім квадратичним відхиленням випадкової величини.

Імовірність того, що нормально розподілена випадкова величина набуде якого-небудь значення з інтервалу , обчислюється за формулою:

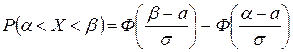. (2.7)

Імовірність того, що відхилення нормально розподіленої випадкової величини від математичного сподівання не перевищить за абсолютною величиною 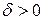, обчислюється за формулою:

. (2.8)

3. ЕЛЕМЕНТИ МАТЕМАТИЧНОЇ СТАТИСТИКИ

Дата добавления: 2015-10-28