Системи з масовим паралелізмом

Ці системи відносяться, по класифікації Фліна, до систем типу MIMD і складають велику конкуренцію конвеєрно-векторним системам. Для створення таких систем, що складаються з декількох сотень зв'язаних процесорів, треба було вирішити ряд проблем, як в апаратних засобах, так і в програмних. Такі системи будуються з вузлів, які зв'язуються з сусідніми вузлами. До складу кожного вузла включаються процесор або група процесорів і власна пам'ять. Якщо використовується група процесорів, то в ній є векторні, скалярні і комутаційні процесори. Паралельні ОС будуються, використовуючи різні типи топологій. Найпростіша з них – лінійка (Рис.6.10).

Рис.6.10.

Недолік: максимальна довжина передачі повідомлень (діаметр системи) залежить від кількості процесорів, тому кількість тут обмежена.

Частіше використовують двовимірні грати, а ще краще – тор (Рис.6.11.).

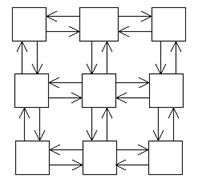
Рис.6.11.

Найоптимальніша структура – n-мірний гіперкуб (Рис.6.12).

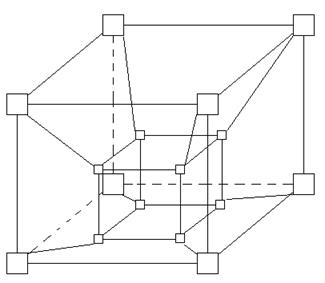
Рис.6.12.

Закон Амдала

Набуваючи для вирішення свого завдання паралельну обчислювальну систему, користувач розраховує на значне підвищення швидкості обчислень за рахунок розподілу обчислювального навантаження по безлічі паралельно працюючих процесорів. В ідеальному випадку система з n процесорів могла б прискорити обчислення в n разів. У реальності досягти такого показника з ряду причин не вдається. Головна з цих причин полягає в неможливості повного розпаралелювання жодної із задач. Як правило, в кожній програмі є фрагмент коду, який принципово повинен виконуватися послідовно і лише одним з процесорів. Це може бути частина програми, що відповідає за запуск задачі і розподіл розпаралельного коду по процесорах, або фрагмент програми, що забезпечує операції вводу/виводу. Можна привести і інші приклади, але головне полягає в тому, що про повне розпаралелювання задачі говорити не доводиться. Відомі проблеми виникають і з тією частиною задачі, яка піддається розпаралелюванню. Тут ідеальним був би варіант, коли паралельні гілки програми постійно завантажували б всі процесори системи, причому так, щоб навантаження на кожен процесор було однакове. На жаль, обидві ці умови на практиці важко реалізовуються. Таким чином, орієнтуючись на паралельну ОС, необхідно чітко усвідомлювати, що досягти прямо пропорційного числу процесорів збільшення продуктивності не вдасться, і, природно, встає питання про те, на яке реальне прискорення можна розраховувати. Відповідь на це питання в якійсь мірі дає закон Амдала.

Джин Амдал (Gene Amdahl) — один з розробників всесвітньо відомої системи IBM 360, в своїй роботі [48], опублікованій в 1967 році, запропонував формулу, що відображає залежність прискорення обчислень, що досягається на багатопроцесорній ОС, від числа процесорів і співвідношення між послідовною і паралельною частями програми. Показником скорочення часу обчислень служить така метрика, як «прискорення». Нагадаємо, що прискорення S — це відношення часу Ts, що витрачається на проведення обчислень на однопроцесорній ОС (у варіанті якнайкращого послідовного алгоритму), до часу Tp рішення тієї ж задачі на паралельній системі (при використанні якнайкращого паралельного алгоритму):

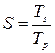
Обмовки щодо алгоритмів рішення задачі зроблені, щоб підкреслити той факт, що для послідовного і паралельного вирішення кращими можуть опинитися різні реалізації, а при оцінці прискорення необхідно виходити саме з якнайкращих алгоритмів.

Проблема розглядалася Амдалом в наступній постановці (Рис.6.13.). Перш за все, об'єм вирішуваної задачі із зміною числа процесорів, що беруть участь в її рішенні, залишається незмінним. Програмний код вирішуваної задачі складається з двох частин: послідовною і такою, що розпаралелює. Позначимо частку операцій, які повинні виконуватися послідовно одним з процесорів, через f,

де 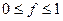(тут частка розуміється не по числу рядків коду, а по числу реально виконуваних операцій). Звідси частка, що доводиться на частину програми, що розпаралелює, складе 1 - f. Крайні випадки у значеннях віповідають повністю паралельним (f = 0) і повністю послідовним (f =1) програмам. Частина програми, що розпаралелюється, рівномірно розподіляється по всіх процесорах.

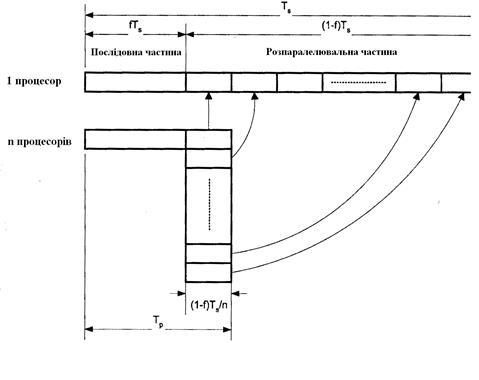
Рис.6.13. До постановки задачі в законі Амдала

З урахуванням приведеного формулювання маємо:

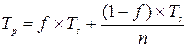
В результаті отримуємо формулу Амдала, що виражає прискорення, яке може бути досягнуте на системі з n процесорів:

Формула виражає просту і таку, що володіє великою спільністю залежність. Характер залежності прискорення від числа процесорів і частки послідовної частини програми показаний на рис.6.14.

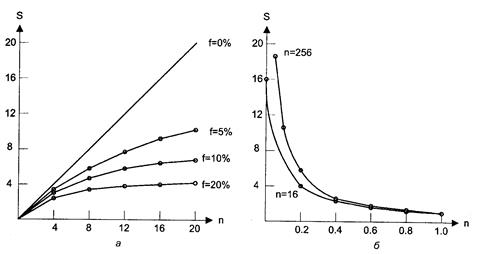
Рис.6.14. Графіки залежності прискорення від: а — долі послідовних обчислень; б — числа процесорів

Якщо спрямувати число процесорів до нескінченності, то в границі отримуємо:

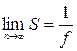
Це означає, що якщо у програмі 10% послідовних операцій (тобто f =0,1), то, скільки б процесорів не використовувалося, прискорення роботи програми більш ніж вдесятеро ніяк не отримати, да і то, 10 — це теоретична верхня оцінка самого кращого випадку, коли ніяких інших негативних чинників немає. Слід зазначити, що розпаралелювання веде до певних витрат, яких немає при послідовному виконанні програми. Як приклад таких витрат можна згадати додаткові операції, пов'язані з розподілом програм по процесорах, обмін інформацією між процесорами і так далі.

Дата добавления: 2015-10-28