Символический метод расчёта

Другим методом расчёта является символический метод – представление векторов в виде комплексных чисел.

Комплексное число (назовём здесь его Z) имеет действительную и мнимую части. Назовём их R и X. Запись числа в алгебраической форме:

Z = R+jX,

Где j = √-1– «мнимая единица». j² = -1. В математике также обозначается не j, а буквой i.

Комплексное число может быть представлено векто-ром (или точкой) на комплексной плоскости, где по оси ординат откладывается действительная часть, а по оси абсцисс – мнимая часть (рисунок 2.4).

Именно так в дальнейшем будут обозначаться сопротивления:

R – активное сопротивление;

X – реактивное сопротивление;

Z – полное сопротивление.

Далее эти понятия (R, X, Z) будут изучаться детально.

Существует также показательная форма записи комплексных чисел:

Z = ‌‌Ze^jφ ‌

Перевод из одной формы в другую производится, используя формулы Эйлера:

e^jφ = cos φ + j sin φ

e^-jφ = cos φ - j sin φ

Ещё одна форма записи – тригонометрическая:

Z = Z cos φ + j Z sin φ

Формулы перевода из одной формы в другую имеют вид:

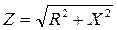φ = arctg X/R R = Z cos φ X = Z sin φ

‌‌

Z = R + jX

Аналогично в символической (комплексной) форме записывается ток и напряжение:

İ = I e^jψi, Ú = U e^jψu

Выражение для комплексов тока и напряжения обычно записываются через действующие значения, но могут быть также записаны и через амплитудные:

İ_m = I_me^jψi, Ú_m = U_me^jψu

Пояснения к обозначениям. Может возникать путаница при одинаковых обозначениях, например: I – «комплекс тока» и I – «действующее значение тока». То же касается Z и U. Поэтому для символического обозначения комплексного числа нужно использовать другое обозначение. Для функции времени – напряжения и тока – используется обозначение с точкой вверху. Сопротивление Z не является функцией времени, поэтому обозначать его Ż ошибочно. Для сопротивления принято для комплекса обозначение с подчёркиванием снизу: Z.

Для операций сложения (вычитания) удобна запись комплекса в алгебраической форме, для умножения (деления) – в показательной. При выполнении расчётов вручную, часто приходится преобразовывать одну форму в другую, что является довольно громоздким и трудоёмким.

Активное сопротивление в цепи переменного тока

Рисунок 2.5 - Резистор в цепи переменного тока

На рисунке 2.5 показана простейшая цепь с резисто-ром, подключённым к синусоидальному напряжению.

U_R(t) = U_msin (ωt+ψ_u) = i(t) R

i_R(t) = U_m/R sin (ωt+ψ_u) = I_msin (ωt+ψ_i)

ψ_u = ψ_i

I_m=U_m/R или, для действующих значений, I = U/R – закон Ома.

В комплексной форме закон Ома: Ú = İ Z

В данном случае - Z = R, Ú = İ R

Комплексное сопротивление в этой цепи является чисто действительным числом, мнимая часть сопротивле-ния равна нулю – Х = 0 и R называется активным сопротивлением.

Угол φ = ψ_u-ψ_i – называется сдвигом фаз между током и напряжением.

В цепи с активным сопротивлением R сдвиг фаз между током и напряжением равен нулю:

φ = 0, ψ_u = ψ_i

Вектора тока и напряжения совпадают по направлению. Совпадают также формы тока и напряжения.

Дата добавления: 2015-10-26