Соединение сопротивлений

Во многих случаях расчёт электрической цепи можно упростить, путём преобразования её из сложного вида в более простой. При этом уменьшается число узлов, ветвей либо и то и другое.

Необходимое условие преобразования: токи и напряжения в остальных частях схемы, не подвергающих-ся преобразованию, не изменяются. Такое преобразование называется эквивалентным.

а) Последовательное соединение сопротивлений

Последовательное соединение – это такое, при ко-тором во всех элементах цепи течёт одинаковый ток. Элементы ветви соединены последовательно (рис. 1.6).

Такую ветвь можно заменить одним резистором с сопротивлением R_экв, равным сумме сопротивлений всех резисторов.

R_экв = = R₁+R₂+R₃+…+R_n

Эквивалентное сопротивление при таком соедине-нии всегда больше сопротивления любого из элементов. Если все сопротивления равны

R₁= R₂= R₃=…= R, то R_экв = nR

Для проводимостей G формула будет выглядеть так:

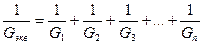
Напряжение на зажимах ab равно сумме напряжений на каждом элементе ветви.

б) Параллельное соединение сопротивлений

Параллельное соединение сопротивлений – это такое соединение, при котором ко всем элементам цепи приложено одинаковое напряжение.

Параллельно соединены элементы между двумя узлами (рисунок 1.7).

Ток I в неразветвлённой части равен сумме токов в каждом элементе.

I = I₁= I₂+ I₃+…+ I_n

Эквивалентная проводимость в этом случае равна сумме проводимостей всех элементов:

G_экв = = G₁+ G₂+ G₃+…+ G_n

Для сопротивлений R формула будет выглядеть так:

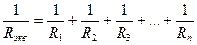
Как видите, формулы симметричны: при последова-тельном соединении складываются сопротивления, а при параллельном – проводимости.

Эквивалентное сопротивление при таком соедине-нии всегда меньше сопротивления любого из элементов.

Если все сопротивления равны R₁= R₂= R₃=…= R, то

R_экв = R/n

Ток в любой ветви пропорционален проводимости этой ветви.

в) Смешанное соединение сопротивлений

Смешанное соединение сопротивлений – это такое соединение, которое можно представить в виде параллельного и последовательного.

На первый взгляд кажется, что любую схему соединения элементов можно представить в виде смешанного соединения и найти эквивалентное сопротивление путём преобразования параллельных и последовательных участков. Однако бывают случаи, когда соединение элементов не является смешанным. Примером такого случая может служить распространённая в электронике мостовая схема, показанная на рисунке 1.8.

Как найти сопротивление между точками a и d? После нескольких попыток упростить схему, легко убе-диться, что здесь нет участков ни с последовательным, ни с параллельным соединением. Для этого нужно приме-нить преобразование, описанное в следующем параграфе.

г) Преобразование «Звезда-треугольник»

Существует возможность эквивалентного преобра-зования треугольника сопротивлений, показанного на ри-сунке 1.9, в трёхлучевую звезду (рисунок 1.10).

При преобразовании одной схемы в другую, напря-жения и токи, как при любом эквивалентном преобразова-нии, не изменяются.

Формулы для преобразования из треугольника в звезду:

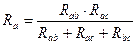
Формулы для преобразования из звезды в треугольник:

R_ab = R_a+ R_b+ R_aR_b/R_с

R_ac = R_a+ R_c+ R_aR_c/R_b

R_bc = R_c+ R_b+ R_cR_b/R_a

Если все сопротивления равны, то легко убедиться, что сопротивления в треугольнике в три раза больше, чем в звезде.

Теперь вернёмся к мостовой схеме на рисунке 8. Можно преобразовать в ней треугольник abc в звезду. Получим схему на рисунке 1.11.

В этой схеме сопротивления треугольника R₁, R₂, R₃ преобразованы в звезду R_a, R_b, R_c.

Теперь не вызывает затруднения найти сопротивле-ние R_ad. Для этого нужно найти последовательные соеди-нения Rb-R4 и Rc-R5, затем параллельное соединение двух получившихся и затем - последовательное соедине-ние с R_a.

Также и в других подобных случаях преобразование «звезда-треугольник» может быть незаменимым.

Дата добавления: 2015-10-26