Глава 6 Метод узловых напряжений

(узловых потенциалов)

Ещё один метод расчёта цепей – метод узловых напряжений (метод узловых потенциалов). В качестве неизвестных промежуточных величин принимаются напряжения (или потенциалы) в узлах схемы.

Рассмотрим схему на рисунке 1.23.

В схеме три узла (не показалось ли вам, что их четыре?) – обозначенных числами 1, 2, 3. Потенциал каждого узла: φ₁, φ₂, φ₃. Напряжения между ними:

U₁₂=φ₁ - φ₂ (напряжение U₁₂ направлено от узла 1 к узлу 2)

U₁₃ = φ₁ - φ₃

U₂₃ = φ₂ - φ₃

В схеме играют роль не сами потенциалы, а их разность – напряжение. Примем потенциал одного узла, например 3, равным нулю - φ₃=0. Так часто делается в электронике – называется «общий провод». Таким образом, между величиной напряжения и потенциала нет никакой разницы:

U₁₃= φ₁ = U₁

U₂₃= φ₂ = U₂

U₃ = φ₃ = 0

При расчёте схемы за неизвестные примем напряже-ния (или потенциалы, что безразлично) узлов. Число уравнений такое же, как по первому закону Кирхгофа, в данном случае – два, так как узлов – три. Понятно, что если известны два потенциала, то легко найти и третий. Искомыми напряжениями будут U₁ и U₂.

Для составления уравнений введём новые понятия.

Собственная проводимость узла G_ii – сумма про-водимостей всех ветвей, подключённых к этому узлу. При этом нужно учитывать проводимости источников энергии.

Источник ЭДС – R = 0, G = ∞;

Источник тока - R = ∞, G = 0; (G = 1/R)

В данной схеме:

G₁₁ = G₁ + G₂ + G₃

G₂₂ = G₃ + G₄

(проводимость ветви с источником тока равна нулю)

Общая проводимость двух узлов G_ik – сумма проводимостей всех ветвей между двумя узлами.

G₁₂ = G₂₁ = G₃

Узел с потенциалом, равным нулю, не учитывается, поэтому получилась только одна величина общей проводимости.

Узловой ток J_ii – алгебраическая сумма токов источников, действующих в ветвях, подключённых к данному узлу i.

При этом необходимо учитывать знак. Если ток, вызываемый источником, подтекает к узлу, то он считается со знаком «плюс», а если вытекает из узла – то «минус».

Ток в ветви с источником тока считается равным J_i. Ток, вызываемый источником ЭДС равен: J_экв = E/R = EG.

В данной схеме:

J₁₁ = E₂G₂ - E₁G₁ = E₂/R₂ - E₁/R₁

J₂₂ = J (источники ЭДС в ветвях узла 2 отсутствуют)

Составляем систему уравнений.

Коэффициенты при собственных проводимостях G_ii положительны, при общих проводимостях G_ik – отрицательны.

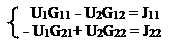
Решаем систему уравнений относительно напряжений.

Теперь определяем токи в ветвях, учитывая направление узловых напряжений и источников ЭДС: если направление источника ЭДС и узлового напряжения совпадают с направлением тока в ветви, то оно берётся со знаком «плюс», если противоположны – со знаком «минус».

I₁ = (E₁+U₁)/R₁= (E₁+U₁)G₁

I₂ = (E₂ -U₁)/R₂ = (E₂-U₁)G₂

I₃ = (U₁-U₂)/R₃= (U₁ -U₂)G₃

I₄ = U₂/R₄ = U₂G₄

I₅ = J – это очевидно

Порядок расчёта методом узловых напряжений

1) Выбираем направления токов в ветвях;

2) Выбираем узел, потенциал которого будем

считать нулевым;

3) Для остальных узлов определяем собственные и

общие проводимости;

4) Определяем узловые токи;

5) Составляем и решаем уравнения;

6) Находим токи в ветвях.

Методы контурных токов и узловых потенциалов являются основными методами расчёта сложных цепей. Оба этих метода получены из законов Кирхгофа и достоинством их является меньшее число уравнений: в методе контурных токов их число такое же, как по второму закону Кирхгофа, а в методе узловых напряже-ний – такое же, как по 1-му закону. Исходя из числа уравнений, и выбирают обычно метод расчёта.

Если количество уравнений одинаково, то всё же проще использовать метод контурных токов. Во-первых, так значительно легче определить токи после решения уравнений, во-вторых, - обычно в условии заданы сопротивления резисторов, а не их проводимости, что влечёт дополнительные вычисления при решении методом узловых напряжений.

Дата добавления: 2015-10-26