Минимизация булевых функций.

А↔{P,O={,&,V,→,~}} – алгебра логики.

P↔{P₁,...,P_n}.

Алгебра – есть объект с разрешенными операциями над ним.

1. Алгебра чисел.

А₁↔{N,C,R,D,{+,-,*,/,...}}, где N, C, R, D – числовые объекты

{+, -, *, /,...} – операции над числами

N – натуральное, C – целое, R – рациональное, D – действительное.

Джордж Буль – английский математик (отец писательницы, написала книгу «Овод», рассмотрел алгебру, которую в честь его называют булевой).

А_б↔{{1,0},{,&,V,→,~,↓,∆,o}}, где {1,0} – объекты.

Буль предложил рассмотреть в качестве чисел только 2 числа 1 и 0, а разрешенные операции над ними не числовые, а логические.

А_б↔{{1,0},{,…o}} сопоставляем.

↓ ↓

А↔{{И,Л},{,…~}}

	x	f0(x)	f1(x)	f2(x)	f3(x)
1)
2)
		f0=0 “const 0”	f1=1 “const 1”	f2=x	f3=x

Взяв 1 аргумент мы получаем 4 функции, которые принимают значение {1,0}.

Поскольку f₀ и f₁ не зависимы от аргумента x, который для них является не существенным, а сами функции называются несущественными зависимыми от x.

f(x₁,x₂,...x_i...x_n) если

f(x₁,x₂,...0...x_n)

f(x₁,x₂,...1...x_n)

то говорят, что задана функция несуществующая зависящая от x.

x_i – называется несуществующим аргументом.

	x1	x2	f0(x1,x2)	f1	f2	f3	f4	f5
			f0↔0	f1↔1	f2=x1	f3=x2	f4=x1&x2	f5=x1Vx2

f6	f7	f8	f9	f10
f6=x1→x2	f7=x1~x2	f8=x1↓x2	f9=x1/x2	f10=x1∆x2

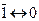
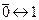
f₈ → операция Вебба (x₁ox₂)

↓

операция Пирса (x₁↓x₂) – чаще употребляется.

f₉ – операция Шеффера (x₁/x₂)

f₁₀ – операция по модулю 2(mod2) (x₁∆x₂).

В булевой алгебре при числе переменных n, то набор 2ⁿ, а число функций .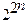

Эти функции (f₀-f₁₀) наряду с рассмотренными функциями для x₁, называются простейшими элементарными функциями булевой алгебры.

Остальные симметрично относительно главной диагонали. Бинарные булевы операции подчиняются законам ассоциативности, коммутативности, дистрибутивности.

1) pVq↔qVp => x₁Vx₂↔x₂Vx₁

2) p&(qVr)↔(p&r)V(p&r) => x₁&(x₂Vx₃)↔(x₁&x₂)V(x₁&x₃)

переписываем все ↔-ти алгебры логики на язык булевских функций.

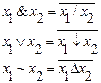
В алгебре Буля можно указать каноническое или стандартное представление функции СДНФ, ДНФ, СКНФ, КНФ.

Рассмотрим базис логических операций в булевой алгебре:

{,&,V,~,→,∆,/,↓}

мы замечаем, что с первыми 5 операциями мы уже познакомились в алгебре логики, рассмотрим последние.

(↓) – стрелка Пирса и (/) – операция Шеффера связаны законами де Моргана.

1. 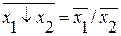это аналоги законов де Моргана.

2.

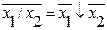
3. если ,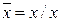

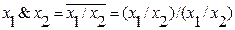
(↓) и (/) называются универсальными, т.к. одной из этих операций можно представить любую булевскую функцию.

(возникает вопрос:)

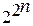функций от n – аргументов

А_n – число функций существующих, зависящих от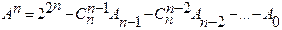

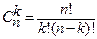число сочетаний, бином Ньютона.

При n=2, A₂=10.

{-,&,V, →,~,∆,↓,/} – базис булевых операций.

Базисом для описанных булевых функций называется R-множество булевых функций, с помощью которых, мы можем описать любую булевскую функцию.

Пусть задано R-множество булевских функций. И задано конечное множество функций вида {f1,...fm}.

Df1. Тогда говорят, что система функции {f₁,...f_m} является базисом, если с помощью этих функций (применяя операции переименования переменных или суперпозиции) мы можем описать любую функцию f из множества .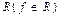

Если мы какую-то функцию f_i опустим, мы уже не получим нужное количество функций для описания f из R.

Базис называется минимизированным, если ин содержит наименьшее число функций для описания функции .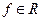

Базис является максимальным, если все множество R не что иное как сами функции.

Стрелка Пирса и оператор Шеффера могут с помощью самих себя описать любую булевскую функцию {/}, {↓}.

Максимальным базисом от функции n-аргументов является полный набор из 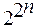функций.

По аналогии с ФАЛ мы можем представить булевы функции в каноническом виде, т.е. в СКНФ или СДНФ, либо в КНФ или ДНФ.

f(x₁,x₂,x₃)_ДНФ=x₁V(x₂&x₃)

f(x₁,x₂,x₃)_КНФ=x₁&(x₂Vx₃)

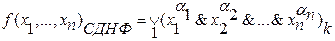, таких выражений будет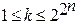

– означает, что входящие элементы конъюнкции берутся только те, при которых функция принимает единичное значение.

	x1	x2	F1
				=х1^0&x2^0= х1&x2
				=х1^0&x2^1= х1&x2
				=х1^1&x2^0= х1&x2
				=х1^1&x2^1= х1&x2

V

1. исходная функция должна быть представлена в виде таблицы своих значений.

2. в таблице значений функций отмечаются те наборы аргументов, на которых функция равна 1 (в данном случае это 1,2,4).

3. каждое единичное значение функции расписанное в виде элементарной & переменных.

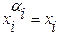, если α_i=1

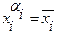, если α_i=0 – конкретное значение переменной.

4. собираем из знаков дизъюнкции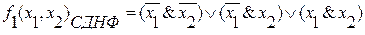

В СДНФ можно представить любую функцию, кроме функции тождественно-равной 0.

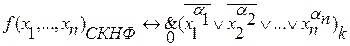
В CКНФ мы не можем представить лишь функцию ↔ И.

1. Исходная функция должна быть представлена в виде таблицы своих значений.

2. В таблице значений функций отложим те наборы аргументов, где функция принимает нулевое значение.

3. Каждое из нулевых значений распишем в виде элементарной дизъюнкции, по следующему правилу:

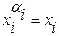, если α_i=0

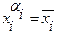, если α_i=1

и получим элементарную V соединенную знаком &.

Рассмотрим по предыдущей переменной:

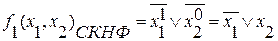
Пример:

(&) заменим на (.)

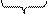
добавим для доказательства

т.к. при этом ничего не изменится (xVx↔x)

объединяем 1-ую и 2-ую, 3-ую и 4-ую,

5-ую и 6-ую.

Мы рассмотрели задачу минимизации на примере, а теперь рассмотрим формально. Задачу минимизации будем рассматривать в классе ДНФ.

Df1. рангом элементарной конъюнкции 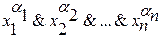называется членом, который раньше мы называли длиной.

Df2. ДНФ функция называют ее представленной в базисе {,&,V} с помощью дизъюнкции элементарной конъюнкций ранга ≤ R.

Df3. длиной ДНФ называют число элементарной конъюнкции ранга ≤ n.

Df4. CДНФ есть ДНФ, где все элементы конъюнкции имеют ранг = n.

Df5. 1. минимизация ДНФ (сокращено МДНФ) называют такое представление булевых функций, которое содержит min число букв для описания исходной булевой функции (см. предыдущий пример, где последняя запись x₁Vx₂x₃ – есть МДНФ).

2. постановка задачи min является сокращение числа логических операций.

3. постановка – является сокращение одновременно и числа букв и числа операций, это постановка получила название абсолютной минимизации.

Замечания:

всего более 600 методов минимизации, при наличии более 3-х переменных для решения задач минимизации используют машины. Нет универсального алгоритма минимизации функций, а есть алгоритмы для минимизации отдельных классов функций.

Дата добавления: 2015-09-01