Читайте также:
|
Если k=n, то мы получили нульместный предикат, т.е. подставляя все n переменных, получили высказывание.
S(x,y,z)↔x+y=z
3-местный предикат
, если x=2, то получаем S(x,y,z)↔2+y=z – 2-х местный предикат.
Если подставить все 3 переменные, то получим S(x,y,z)↔2+3=5 – получили высказывание, нульместный предикат или вырожденный предикат.
Все операции, которые мы можем выполнить над высказыванием, => переместим в исчисление предикатов.
1. Отрицание.
Свойством P(x), мы разбиваем множество 
на 2 подмножества: удовлетворяющему свойству P(x) и не удовлетворяющему свойству 
множество x отвечает этому свойству,
– множество x, не обладающие этим свойством.
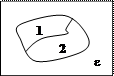
область 1
область 2
Если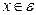 
, т.е. рассмотрим универсальное множество.
дополнение – теоретико-множественный знак.
– отрицание свойства – это логический знак отрицания.
Позволяет перейти от основного множества к дополнению.
2. Конъюнкция.
P(x)&Q(x) – это свойства
Переменная x должна отвечать 2 свойствам P и Q.
.
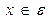- область 1
- область 2
3. Дизъюнкция.
P(x)VQ(x)
Для переменной x заданы 2 свойства, x должен обладать хотя бы одним из этих свойств.
4. Импликация (→).
Наличие свойства P для переменных x влечет за собой свойство Q.
(по свойству 
).
5. Эквивалентность (~).
(по свойству 
).
операция – упорная (), а &, V, →, ~ -
это бинарные операции.
С помощью предикатов мы рассмотрели как свойства объектов, так и отношение между ними.
Дата добавления: 2015-09-01; просмотров: 39 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Формулы исчесления предикатов. | | | Равносильные формулы в исчислении предикатов. |