Способы вычисления ФАЛ.

Когда говорят, что нужно вычислить ФАЛ от n переменных то говорят, что нужно указать ее таблицу значений в таблице истинности. Количество строчек 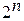, где n - число участвовавших логических переменных.

	…
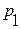
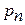
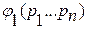
И Л Л И И Л	. . . . . .	И Л . . И Л	И(Л) . . . . И(Л)

Выписываем конкретные значения функции в правой колонке таблицы истинности (мы указали лишь одну из них).

возможных логических формул.

Количество значений логических переменных 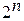, а в каждой строчке функция принимает тоже одно из двух значений 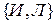, т.е. число возможных значений .

Существует 2 способа вычисления функции алгебры логики:

1 способ: последовательный. Выполняются логические операции на всем наборе переменных последовательно соблюдая порядок действий.

Рассмотрим пример:

№
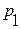
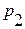
	И И И И Л Л Л Л	И И Л Л И И Л Л	И Л И Л И Л И Л	И И Л Л И И И И	И Л Л Л И Л Л Л	И И Л Л И И И И	Л Л Л Л И И И И	Л Л И И И И И И

Выделяем очередность операций.

Для облегчения записи значений логических переменных употребляют запись в двоичной системе: значение «И» – записывают через 1, а «Л» – через 0. Все № строк записываются в двоичной системе счисления: (№…)_{10 с/с} → (№…)_{2 с/с}

2 способ: параллельный. Одновременно выполняются все участвующие операций на заданном наборе переменных.

Рассмотрим тот же пример, что и в первом способе. Во-первых, также указываем последовательность выполнения операций. После этого берем одну (например, первую) фиксированную строчку и определяем все операции для нее, т.е. в конечном счете в этой строчке получаем конкретное значений функции. Указанная процедура проводится во всех строчках значений переменных.

Иногда первый способ называется вычислением функций по столбцам, второй способ – вычислением функции по строчкам. Независимо от выбора способа вычисление ФАЛ получается одно и то же значение функции.

Выбор способа вычисления ФАЛ определяется конкретными условиями задачи. Например, если требуется указать хотя бы одно значение функции, то необходимо применить второй способ.

Дата добавления: 2015-09-01