Проблема разрешения.

В алгебре логики существует так называемая проблема разрешения, которая заключается в следующем: имеется исходная формула некоторой ФАЛ . Необходимо ответить на вопрос, является ли данная форма тождественно истинной, т.е. принадлежит ли она 1 классу ФАЛ.

╞^? , φ(р₁,…,р_n) ≡ И обозначим ╞ φ.

Ответом на поставленный вопрос фактически является процедура вычисления ФАЛ одним из указанных выше способов. Если при вычислении получаются только истинные значения функции, то данная формула относится к классу тождественно-истинных, если получается хотя бы одно из значений ложное, то данная формула не является тождественно-истинной ()

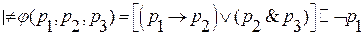
Данная формула не является тождественно-истинной, т.к. в последней колонке таблицы истинности имеются 2 значения – ложно.

Приведем пример тождественно-истинной функции.

╞

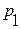
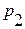
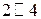
№									φ(р1,р2,р3)
	И И И И Л Л Л Л	И И Л Л И И Л Л	И Л И Л И Л И Л	И Л И Л И И И И	И Л И И И И И И	И И Л Л Л Л Л Л	И Л И И И И И И	И И И И И И И И	. . . . . . . .

Дата добавления: 2015-09-01