Функции алгебры логики (ФАЛ).

(функции алгебры высказываний)

Построить таблицу истинности функции алгебры логики f (p₁,…,p_n)

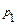
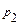
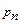
		…		f (p1,…,pn)
И И . . Л	И И . . Л	… … . . .	И Л . . Л	И(Л) И(Л) И(Л) И(Л) И(Л)

	2^n строк

, , …, ,

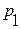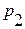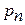
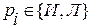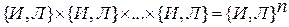– декартова степень.

n

С помощью логических констант, фиксируем определенную строку и определенную формулу: φ (p₁,…,p_n)

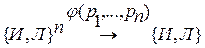или φ (p₁,…,p_n): {И, Л}ⁿ→{И,Л}.

Df1. Функция, где 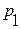,…, 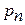есть логические переменные, принимающие одно из 2 значений: 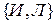, отображающая множество 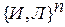на множеств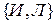о , то 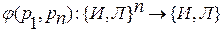называется n-местной (n – число логических переменных) высказывательной функцией ФАЛ от n – логических переменных, или допускается название логической функции от n переменных.

В тех случаях, когда не важен способ представления функции (записывается в виде таблицы истинности, или в аналитической форме) разрешено одними и теми же буквами обозначать и логическую формулу и ее логическую формулу.

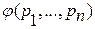- логическая формула описывает соответствующую логическую функцию: f (p₁,…,p_n).

Там, где следует подчеркнуть, что имеем дело с функцией, то вводят для функции специальные обозначения 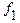, …, , ,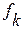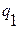…, 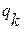и т.д.

Замечание (относительно отображения).

1) Отображение взаимно-однозначное, т.е. для каждого фиксированного значения логических переменных имеется одно из 2 возможных значений функции.

2) Одна и та же логическая функция может быть записана бесконечным множеством равносильных формул.

В то же время все равносильные формулы описывают одну и ту же функцию.

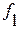- логическая функция.

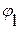
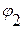
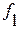- функция.

…

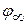- равносильные логические формулы.

Df2. Две логические формулы 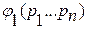и 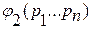, описывающие или определяют логическую функцию 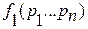, называются равносильными.

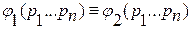- формулы.

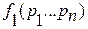- функция.

Примеры:

1)

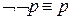
2)

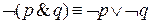
Все предыдущие законы, указанные как свойства логических операций есть примеры равносильных формул.

Логические переменные

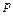
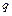
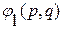
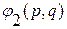
	И И Л Л	И Л И Л	Л И И И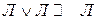

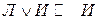
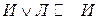
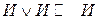
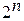
Из определения операции эквивалентности и равнозначности вытекает следующее утверждение.

Утверждение 1. Если 2 формулы 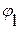и 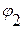равносильны (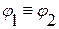), то они эквивалентны (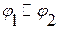) и наоборот.

Доказательство:

а) ,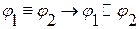

в) .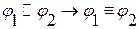

Из этого утверждения во всех ранее указанных законах знак заменить на знак 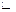(эквивалентность), получим новое выражение, которое будет являться формулой.

1) , ,

,

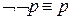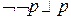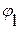
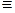
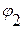2) , ,

, .

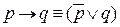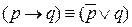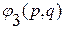Заменой знака 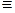на знак 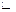мы указываем один из способов получения новых формул из уже заданных.

Способы образования новых ФАЛ.

1) заме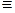на на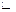

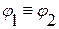
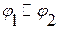
Позволяет произвести обратную замену, т.е. заме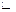на на .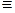

2) Подстановка вместо логических переменных новых формул.

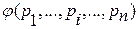- логическая формула.

Вместо каждой из 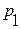,…, ,…, 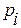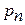можно подставить формулу.

Например, вместо 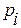подставим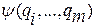

Пример:

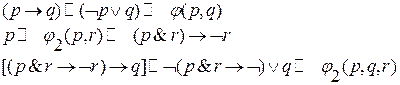
3) Замена логических переменных новыми логическими переменными (способ подстановки логических переменных).

Пример:

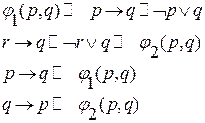
Независимо от способа образования новых формул все множество логических функций можно разделить на 3 класса.

1 кл. Тождественно-истинные формулы (функции) «И» ╞ φ, φ ≡ И

2 кл. Выполнимые или нейтральные формулы (функции) хотя бы 1 значение «И» и «Л»

3 кл. Тождественно-ложные формулы (функции) «Л» φ ≡ Л

1 кл. на всевозможные значения логических переменных принимает только истинные значения.

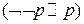
3 кл. на все возможные значения логических переменных принимает только ложные значения.

Примеры тождественных преобразований логических формул.

Для тождественных логических преобразований формул используются ранее указанные законы логических (формул) операций.

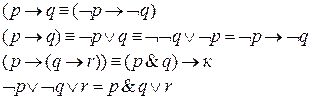
Дата добавления: 2015-09-01