Кванторы.

Рассмотрим пример:

1) , если все элементы из множества А входят во множество В. Элемент x будучи заданным во множестве А появляется в множестве В.

Формальная запись выражения 1.

2)

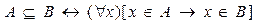
– квантор общности (для всех, или для каждого) x, стоящего под знаком квантора называется связной переменной.

Область действия квантора – это все то выражение, которое идет за квантором.

Разрешим следующую запись:

– квантор x ограничен каким-то свойством общности x, называется ограниченным квантором общности.

!!квантор всегда заключен в скобки!!

Когда нам необходимо выделить значение переменной, соответствующий определенному свойству, используем квантор существования.

Пример:

P(x)↔”x+2=7”

Тот факт, что существует такое x, что x+2=7, можно записать следующим образом в логической форме.

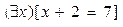, т.е. [x+2=7] – область действия квантора.

– квантор существует.

x – связная переменная.

Разрешим следующую запись:

– ограниченный квантор существует.

!!квантор всегда заключен в скобки!!

Пример:

рассмотрим случай, когда используется оба квантора lim_n→∞a_n=b.

Для любого положительного ε, существует такое число n_ε, связанное с ε, что для любого числа , как только n > n_ε, то |a_n – b| ≤ ε.

С помощью кванторов и предикатов мы можем сами анализировать выражение.

Дата добавления: 2015-09-01