Интерпретация алгебры логики в теории конечных автоматов.

Автоматы: Устройства для дискретной переработки информации (фактически – для переработки чисел)

Конечные автоматы – устройства, использующие конечные алфавиты – это есть универсальные ЦВМ.

Рассмотрим 2 задачи:

1. задача синтеза конечного автомата.

2. задача анализа конечного автомата.

1. Задача синтеза конечного автомата заключается в построении функциональной схемы конечного автомата по его исходному математическому описанию, которое задается на языке ФАЛ. Говорят, что автомат моделирует исходную логическую функцию (отрабатывает).

Примеры синтеза конечных автоматов.

Пусть задана некоторая функция, определяющая синтезируемый конечный автомат.

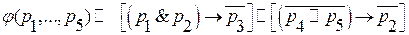
Функциональная схема в ней выделяет все важнейшие функции. Прежде чем синтезировать конечный автомат заранее договариваются о логическом базисе синтезированных функций, задают логические операторы моделирования элементарных логических функций.

{, &, ν, →, ~}.

Рисуют черный ящик, т.е. не знают что находится в черном ящике.

1)

Р

р → (р) → р – инверсия.

2)

&

Р₁ φ(Р₁,Р₂)=Р₁&Р₂

Р₂

логический оператор моделирует логическую функцию: на входе 2 переменных, на выходе постоянное логическое произведение.

3)

→

Р₁ φ(Р₁,Р₂)=Р₁→Р₂

Р₂

на первом входе должно быть р₁, а на 2 входе р₂, если наоборот, то на выходе р₂ → р₁.

4)

~

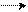Р₁ φ(Р₁,Р₂)= (Р₁ ~ Р₂)

Р₂

для синтеза соответственной функциональной схемы достаточно рассмотреть список операций исходной ФАЛ.

Задача минимизации конечного автомата сводится к минимизации исходной ФАЛ.

Задача синтеза конечного автомата с минимальным количеством переменных.

2. Задача анализа заключается в построении математического описания по функциональной схеме.

Конечный автомат (КА): [(p₁ & p₂) ~ p₃] → p₃

φ (р₁, … р₅) = {[(р₁&p₂) ~ p₃] → p₃} & [p₃ ~ (p₄ V p₅)]

При анализе КА также решить задачу минимизации, является ли полученная конечная логическая функция минимальной, если да, то считается, что схема имеет минимальное число логических операторов.

Дата добавления: 2015-09-01