Интерпретация алгебры логики в теории множеств.

Возникает вопрос, нельзя ли законы математической логики формально перенести в алгебру множеств.

1) 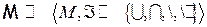- алгебра множеств.

2) 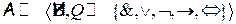- алгебра логики.

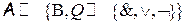
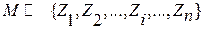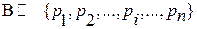] , , где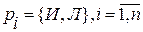

Введем следующий переход:

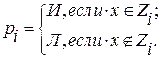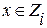, то мы скажем, что 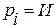, если 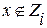, то мы скажем, что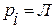

1) Закон коммутативности в алгебре множеств. Если использовать переход, то получим:

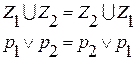2)

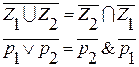
Легко видеть, что можно сопоставить:

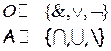
Пример:

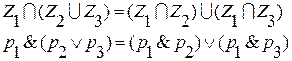
Вывод: Все тождества алгебры множеств можно переписать в терминах алгебры логики и наоборот.

Дата добавления: 2015-09-01