Предикаты.

Предикат – есть свойство объектов или отношение между объектами.

Обозначают предикаты большими буквами и скобками с указанием числа объектов.

Р(*) – унарный – одноместный.

Р(*,*) – бинарный – двуместный.

Р(*,*,…,*) – n-местный предикат.

Предикат, заданный на некотором множестве М[Р], тождественно–истинный, если при любом наборе значений аргументов его значение <=> И и тождественно-ложный, если для любого набора аргументов он <=> Л.

Предикат называется выполнимым, если существует хотя бы один набор значений аргументов, при котором он <=> И.

Два предиката заданные на одном и том же множестве, называют равносильными, если их значение для любого набора переменных совпадают.

Пусть задано два предиката P(x) и Q(x) на одном и том же множестве. Предикат Q(x) называют следствием P(x), если любой набор удовлетворяемый P(x), удовлетворяет Q(x).

Рассмотрим следующий пример.

1. все целые числа – рациональные (p).

2. единица – целое число (q)

=> единица – рациональное число

r

В этом примере мы путем введения 2 посылки входим во внутрь 1 посылки.

p

p&q → r Неизвестно каким путем сделали переход

1. все люди смертны

2. Сократ человек

=> Сократ смертен

Можно сделать вывод: есть ряд высказываний (предложений), которые нельзя доказать с помощью ранее доказанных высказываний, ибо в этих примерах помимо установления истинности или ложности элементарное высказывание требуется анализировать конкретное содержание доказанных предложений.

Устранить отмеченный недостаток позволяет исчисление предикатов (И.П.)

Исчисление предикатов – это есть раздел математической логики, в котором помимо возможности установления истинности или ложности элементарного высказывания имеется возможность установления истинности или ложности высказываний внутри.

Последнее делается при помощи выделения в данном высказывании 2 объектов:

1. субъекта

2. предиката

Субъект – это, то о чем говорится в данном предложении (в предложении – это либо подлежащие либо дополнение)

Предикат – это все то, что говорится о субъекте (в предложении в качестве предиката берется определение или сказуемое)

Субъект – есть некоторый объект, а предикат – обозначение объекта.

Рассмотрим предложение.

Сократ - человек

Сократ – человек

↓ ↓

субъект предикат

Рассмотрим такое предложение.

P(x) ↔ “x – четное число”

P – предикат

x – субъект

x N	P(x)
	И
	И
	И
	Л
	И
	Л

Мы берем x из множества N и пытаемся отобразить его на P(x)

x – четное число.

P – функция отображающая x во множество {И,Л}.

P:x→{И,Л}.

Рассмотрим такое предложение.

Р(x,y)↔”x<y”

C – множество целых чисел.

y x
	Л	И	И	И	И	И	И
	Л	Л	И	И	И	И	И
	Л	Л	Л	И	И	И	И
	Л	Л	Л	Л	И	И	И
	Л	Л	Л	Л	Л	И	И
	Л	Л	Л	Л	Л	Л	И

Мы имеем фактически пару чисел из множества С², т.е. декартова квадрата

↓

это отображает взаимно-однозначное Р:<x,y>→{И,Л}.

Мы построили предикат от двух переменных. Р может задаваться в виде высказывательной формы либо виде таблицы истинности.

Рассмотрим пример:

Берем 3 точки на оси чисел.

x z

y

P(x,y,z)↔точка y лежит между точками x и z на оси чисел.

P:<x,y,z>→{И,Л}

В результате получим предикат от 3 переменных.

Теорема дедукции:

Если правильно умозаключение f₁,f₂,f₃...f_n |– F, то правильно умозаключение

f₁,f₂,f₃...f_n-1 |– (f_n→F) и наоборот.

Теорема не используется для доказательства правильности умозаключения. Зная исходные формулы (ФАЛ) f₁,f₂,f₃...f_n, можно формально получить следствия F_i из них по правилу:

1. составить и привести к КСНФ.

2. взять соответственно по одному, по два и т.д. сомножителей из f и упростить их. Это и будут следствия F_i, всего их 2^к, где к – число членов в КСНФ формулы f.

Df1. n – местным предикатом обозначают Р(x₁,x₂,x₃,...x_n), называют логическая функция от n переменных, осуществим отображен ,где

Если все x_i принимают одну и ту же область, то мы берем n-ку из декартовой n степени множества А, т.е. 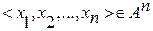, где А₁=А₂=…=А_n.

Дата добавления: 2015-09-01