Методы минимизации булевых функций.

1. Метод неопределенных коэффициентов.

Для простоты рассмотрим этот метод для 3-х переменных.

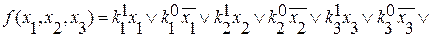индекс означает номер коэффициента, а верхний означает какое значение принимает переменная, возможно 2 вида записи:

1.

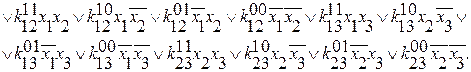
2.

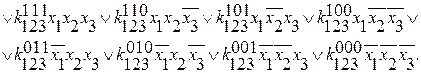
Слева значение функции, в правой части мы видим ДНФ.

Для записи функции необходимо знать значение коэффициента .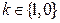

Порядок определения коэффициента следующие:

1. необходимо указать значение аргумента, у которого функция принимает единичные значения или нулевые для этого нужно записать систему уравнений, правая часть которой есть значение функций, а левая часть коэффициенты всевозможных элементарных конъюнкций, полученных из конъюнкций n-го ранга при данном значении функций. Количество уравнений равно 2ⁿ. При совместном решении 2ⁿ уравнений на 1 шаге вычеркиваются коэффициенты построчно, соответствующему 0-му значению функции.

2. на втором шаге в оставшихся строчках вычеркиваются одноименные коэффициенты, вычеркнутые на 1 шаге.

3. среди оставшихся коэффициентов не вычеркнутых строк выбираются коэффициенты соответствующие конъюнкции наименьшего ранга.

Полученные коэффициенты из всей системы соединяются знаком дизъюнкции (V) и для каждого коэффициента расписана соответствующая элементарная конъюнкция, окончательно составленное выражение из элементарной дизъюнкции и есть МДНФ.

Пример:

разбиваем строчную запись на систему уравнений.

f(x₁,x₂,x₃) т.к. коэффициент фактически обозначает значение переменных, то

f(1,1,1) при записи элементарной конъюнкции переменных можно

f(0,1,1) опустить.

↓

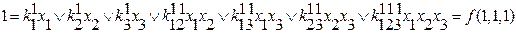
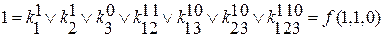
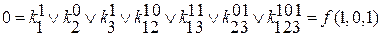
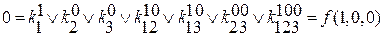
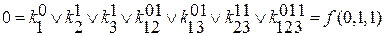
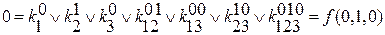
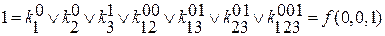
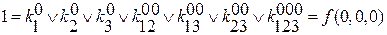
значение функций на кубике

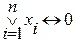, если все x_i принимают значение И.

Выбираем коэффициент меньшего ранга

1)

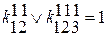
2)

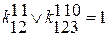
3)

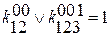
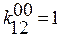
4)

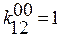
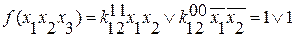
2. Метод минимизирующих карт (Гарвардский метод).

Для простоты рассмотрим этот метод для трех переменных.

1. исходная функция должна быть представлена в СДНФ.

2. составленная и минимизированная карта. Карта содержит 2ⁿ строк, в каждой строке имеется 2ⁿ-1 клеточек, т.о. получаем таблицу (2ⁿ-1)*2ⁿ, где n – число учавствующих переменных.

3. в клеточках данной таблицы расписываем всевозможные элементарные конъюнкции, порядок их записи соответствует записи неопределенных коэффициентов в предыдущем методе.

Построим эту таблицу для 3 переменных. Число строк 2³=8, число столбцов 2³-1=7.

	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3
	x1	x2	x3	x1 x2	x1 x3	x2 x3	x1 x2 x3

x₁x₂x₃↔x₁&x₂&x₃.

Заметим, что запись напоминает нам запись строк предыдущего метода.

4. в построенной минимизированной карте необходимо вычеркнуть строки, соответствующие элементарной конъюнкции наибольшего ранга, отсутствующего в исходной СДНФ.

5. в оставшихся строчках минимизированной карты необходимо вычеркнуть одноименные коэффициенты, попавшие в вычеркнутые строчки предыдущего этапа, т.е. выполнить условие совместности системы элементарной конъюнкции данной минимизированной карты.

6. из каждой не вычеркнутой строчки, среди оставшихся элементарных конъюнкций взять конъюнкции, наименьшего ранга.

7. выборочные элементарные конъюнкции соединить знаком дизъюнкции, (в следствии необходимо сделать приведение подобных, полученное выражение и будет МДНФ заданого ФАЛ).

(если) рассмотрим почему же мы вычеркиваем всю строку. Допустим, что нам дано: x₁, но

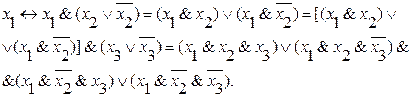
Но если хотя бы 1 элемент из последней записи вычеркивается, то очевидно необходимо вычеркнуть и все элементарные конъюнкции с меньшим числом элементов, ибо если идти в обратном порядке, то мы придем обратно к x1.

Пример:

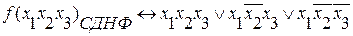
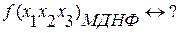
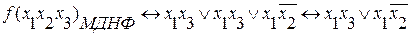
подобные

Возможны несколько видов МДНФ, которые будут отличаться только видом переменных, но не числом.

Как метод неопределенных коэффициентов, так и метод минимизации карт, применим для n_max=5 или 6, при ручном подсчете, при большем числе n они становятся громоздкими. Существует множество методов минимизации, которые выполняются на универсальных машинах.

При анализе и синтезе конечных автоматов и схем, для решения задачи минимизацией необходимо указать функцию в СДНФ, а затем применить один из методов минимизации, полученной МДНФ данной функции, построить функциональную схему конечного автомата, полученная функциональная схема как правило является минимизацией.

Дата добавления: 2015-09-01