Геометрическое представление булевых функций.

f: A→B

ψ ψ

x→y = f(x).

A – область значений аргумента

B – область значений функции

Задавая функции в таблицах истинности, строим функцию по заранее известным значениям простейших функций.

Задавая дискретно значения аргументов, мы получаем четное или дискретное значение функции.

x1	x2	...	xn	f(x1,...,xn)
		...		1(0)
. . .	. . .	. . .	. . .	. . .
		...		1(0)

f

А В

Для наглядности будем строить функцию для 3 аргументов.

Договоримся, чтобы каждая вершина определяла x₁&x₂&x₃, но для простоты будем указывать x₁x₂x₃. если 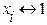, то пишем 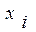, если 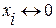, то указываем .

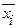Каждой точке будет соответствовать значение функции. Иногда в вершинах указываем значение функции 1 или 0.

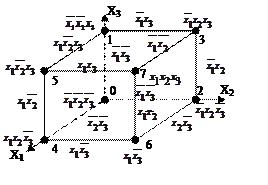Эта картинка может указать, если мы обозначим ребра, то получим, что это общая часть 2 конъюнкций, теперь рассмотрим грани, это 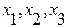, им противоположны грани .

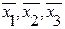Если необходимо отметить вершины, грани и ребра по рангам, то можно отметить. Каждой вершине соответствует конъюнкция 3 ранга – участвует 3 переменных, ребра – конъюнкция 2 ранга – 2 переменных, грани – конъюнкция 1 ранга или сами переменные.

Более того говорят, что конъюнкции меньшего ранга покрывают конъюнкции большего ранга по следующему правилу:

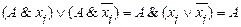
По сути дела мы занимаемся 1 склеиванием ребер, правило склеивания используется во всех методах минимизации.

Выделение 2 области задания функции:

Это множество вершин T₁↔{1}, где функция принимает истинное значение и множество вершин T₀↔{0}, где функция принимает ложное значение.

T↔T₁UT₂ – множество всех вершин единичного куба.

например:

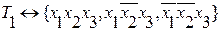– конкретное множество вершин, где функция принимает истинное значение, а остальные вершины очевидно – ложные.

.

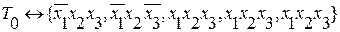Вывод:

Обобщая геометрическое изображение геометрических булевых функций, где n>3, можем сказать следующее для булевых функций необходимо построить единичный n-мерный куб, к вершинам n-мерного куба будут соответствовать вершины n-го ранга, ребрам конъюнкции (n-1)-го ранга, граням (n-2)-го ранга.

Дата добавления: 2015-09-01