Построение вещественной частотной характеристики

При исследовании качества системы частотным методом возникает необходимость в построении графика вещественной частотной характеристики R_з(w) замкнутой системы. Для построения графика можно найти выражение для вещественной частотной характеристики замкнутой системы через передаточную функцию замкнутой системы и затем построить график по точкам.

Для упрощения построения зависимостей используется метод круговых диаграмм, который позволяет построить эту зависимость по известной характеристике разомкнутой системы. Частотные передаточные функции разомкнутой и замкнутой системы можно представить в виде комплексных выражений следующего вида:

где - вещественные частотные характеристики разомкнутой и замкнутой системы соответственно; - мнимые частотные характеристики системы.

Поскольку 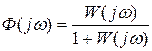, то .

Если принять , то полученное выражение для будет уравнением окружности в координатах . Эта окружность имеет радиус , и её центр расположен на оси вещественных чисел на расстоянии от начала координат. Задавая разные значения константы c, можно получить сетку окружностей на комплексной плоскости частотной характеристики W(jw) разомкнутой системы. Семейство окружностей такого рода получило название круговых диаграмм. Поскольку с использованием круговых диаграмм по характеристике разомкнутой системы определяют характеристику замкнутой системы, то круговые диаграммы называют также номограммами замыкания системы.

Когда годограф W(jw) пересекает окружность с определённым значением c=c_k при частоте w_k, то это означает, что для замкнутой системы . Таким образом, рассматривая точки пересечения АФЧХ разомкнутой системы с окружностями, можно получить последовательность значений координат точек характеристики . По полученным точкам строится вещественная частотная характеристика замкнутой системы.

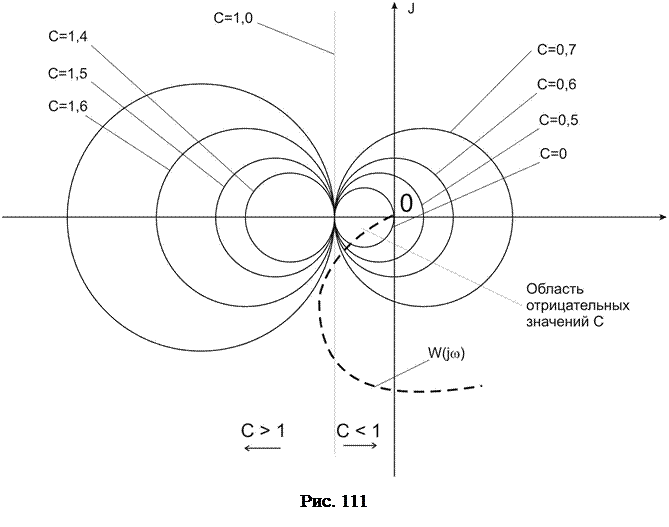
Круговые диаграммы целесообразно вычерчивать на прозрачной бумаге и при построении вещественной частотной характеристики замкнутой системы накладывать на график . Пример использования круговых диаграмм для определения точек вещественной частотной характеристики замкнутой системы показан на рис. 111.

Можно определить по и без построения всех окружностей, используя их свойства пересекаться в точке с координатами . Необходимые для этого построения показаны на рис. 112. Для определения ординаты 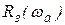вещественной частотной характеристики замкнутой системы для некоторой частоты w_a на годографе помечаем точку A, соответствующую этой частоте. Затем соединяем точку с точкой 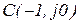и к середине получившегося отрезка 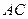(точка В) восстанавливаем перпендикуляр до пересечения с вещественной осью в точке 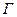, тогда искомое значение ординаты вещественной частотной характеристики при частоте w_a

.

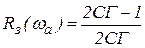Аналогично выпол-няются построения для других точек АФЧХ, что позволяет получить ряд значений для разных частот. По полученным значениям строится график вещественной частотной характеристики замкнутой системы.

Метод круговых диаграмм применим и для нахождения мнимой частотной характеристики замкнутой системы. В этом случае окружности располагаются вдоль оси мнимых чисел.

Дата добавления: 2015-09-02