Читайте также:
|
Если известна передаточная функция замкнутой системы, то можно определить изображение выходного сигнала системы:
.
В случае исследования качества принимаем 
, откуда 
.
Следовательно,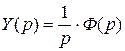 
.
Полученное уравнение справедливо при нулевых начальных условиях системы, т.е. при 
, 
, 
…
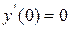Для нахождения функции, описывающей процесс в системе, необходимо осуществить переход в область оригиналов:
.
Полученное решение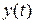 
позволяет построить график переходного процесса в системе и оценить ее качество.
Если система находится при начальных условиях, отличных от нулевых, то изображение Лапласа для производной k-порядка
, где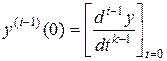 
содержит эти начальные условия. Уравнение системы в изображениях
,
.
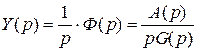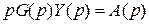С учетом начальных условий 
.
Обозначим 
, тогда 
или 
и .
В полученном решении учтены ненулевые начальные условия системы.
Дата добавления: 2015-09-02; просмотров: 52 | Нарушение авторских прав
| <== предыдущая страница | | | следующая страница ==> |
| Аналитическое решение дифференциального уравнения | | | Численное решение дифференциального уравнения |