Построение области устойчивости системы методом D-разбиения

Рассмотренные критерии устойчивости позволяют ответить на вопрос, является ли рассматриваемая система устойчивой. Однако на практике часто приходится решать задачу о влиянии тех или иных параметров системы на ее устойчивость и о допустимых пределах изменения этих параметров без потери устойчивости системой. Изменение параметров может быть вызвано технологическими допусками при изготовлении системы, ее старением, заменой элементов системы при ремонтах и т.д.

Построение области устойчивости может вестись в пространстве одного или двух параметров. При построении области устойчивости в зависимости от одного параметра обычно исследуется влияние на устойчивость коэффициента усиления системы, рассматриваемого как комплексная величина. Область устойчивости в этом случае строится на комплексной плоскости.

Наиболее часто используется построение области устойчивости в плоскости некоторых двух параметров системы. Пусть представляет интерес оценка некоторых параметров T_i и k_j звеньев системы с точки зрения их влияния на устойчивость. В этом случае можно, задавая разные значения этих параметров, многократно исследовать устойчивость системы при каждом заданном их сочетании. Если результаты таких исследований нанести на график (рис. 91), построенный в плоскости исследуемых параметров T_i и k_j, используя разные обозначения случая устойчивой системы (´) и неустойчивой системы (○), то на графике можно будет выделить некоторую область сочетаний исследуемых параметров, которая будет соответствовать устойчивости системы. Эта область называется областью устойчивости системы.

В соответствии с условием устойчивости САУ (левое расположение корней характеристического уравнения САУ на комплексной плоскости корней) граница области устойчивости будет отделять случай сочетания исследуемых параметров, дающий все левые корни характеристического уравнения, от случаев, когда среди этих корней могут быть и правые корни.

Выделение на плоскости влияющих параметров областей их значений, которые соответствуют разным сочетаниям левых и правых корней характеристического уравнения, называется D-разбиением. Границы этих областей называют D-кривыми. При построении границы устойчивости мы имеем дело с частным случаем D-разбиений, когда нас интересует только одна D-кривая, отделяющая случай всех левых корней характеристического уравнения от других случаев.

Задача построения области устойчивости в плоскости двух параметров сводится к последовательному выполнению двух действий:

· построение линий, соответствующих граничной устойчивости системы в плоскости влияющих параметров,

· определение расположения области устойчивости относительно построенных границ.

Для определения границ области устойчивости можно использовать различные критерии устойчивости. Наиболее широкими возможностями обладает критерий Михайлова, при этом колебательной границе области устойчивости соответствует равенство нулю характеристического комплекса замкнутой системы:

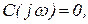или и .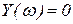

Две другие границы устойчивости могут быть получены из условий

где - первый и последний коэффициенты характеристического полинома замкнутой системы.

При построении области устойчивости в плоскости двух параметров системы определяется характеристический полином замкнутой системы, в котором исследуемые параметры kj и Ti представлены в виде переменных, а все остальные постоянные параметры - в виде констант .

Затем подстановкой характеристический полином преобразуется в характеристический комплекс

.

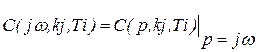Условию нахождения системы на границе устойчивости соответствует равенство нулю характеристического комплекса (кривая Михайлова при этом проходит через начало координат): .

Комплексное выражение будет равно нулю при равенстве нулю его вещественной Х и мнимой Y частей, следовательно, уравнение распадается на два:

Решая последние уравнения относительно исследуемых параметров 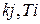, можно в результате получить параметрические уравнения границы устойчивости:

и затем построить по точкам эту границу в координатах , задавая ряд значений параметра 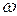в пределах . Результаты вычисления значений параметров 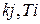сводятся в таблицу, по которой затем строится график кривой, являющейся границей области устойчивости (колебательного типа) в плоскости параметров 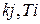(рис. 92). Граница области устойчивости может иметь разрывы и пересекать оси координат.

Для определения расположения области устойчивости относительно построенной границы колебательного типа используется правило штриховки. В соответствии с этим правилом вычисляется определитель вида

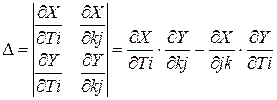
и определяется знак определителя. Если , то при движении по границе устойчивости в направлении возрастания частоты следует штриховать левую сторону границы. При штриховка в тех же условиях ведется справа. При соблюдении этого правила штриховка всегда будет направлена внутрь области устойчивости.

Правило штриховки будет корректным в том случае, когда параметр, по которому берется первая производная определителя (в нашем случае параметр ), на графике области устойчивости откладывается по оси абсцисс (рис. 92). Построенную границу области устойчивости при штриховке необходимо проходить в области изменения частоты . При этом отдельные участки границы области устойчивости могут иметь двойную штриховку.

Граница, определенная на основе критерия Михайлова, является границей колебательного типа. На график следует нанести дополнительные границы области устойчивости, которые находятся путем приравнивания нулю первого и последнего коэффициентов характеристического уравнения системы:

,

.

Из этих уравнений определяются уравнения дополнительных границ области устойчивости. Дополнительные границы наносятся на график области устойчивости. Штриховка дополнительных границ выполняется "по смыслу" в соответствии со штриховкой границы колебательного типа.

Пример. Пусть имеется система, для которой известна передаточная функция разомкнутой системы

,
где K – коэффициент усиления разомкнутой системы. Необходимо построить область устойчивости системы в плоскости параметров: коэффициент усиления K – постоянная времени T₂.

Для решения задачи прежде всего найдём передаточную функцию замкнутой системы:

и запишем характеристический полином замкнутой системы

.

Преобразуем характеристический полином в характеристический комплекс:

.

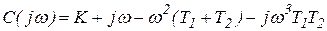Запишем условия для граничной устойчивости системы:

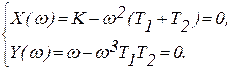
Из уравнений граничной устойчивости найдем параметрические уравнения границы области устойчивости:

; .

Рассчитываем точки границы устойчивости, координаты которых сводим в таблицу.

w		w1	…	¥	-¥
T2	¥	…	…
K	1/T1	…	…	¥	¥

Число точек в таблице должно быть достаточным для выявления всех особенностей границы устойчивости.

Для применения правила штриховки найдем определитель

, , , , .

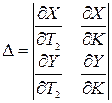Таким образом,

при .

Следовательно, определитель положителен для положительных частот и штриховка должна вестись слева от кривой при движении по ней в сторону возрастания частот. Для отрицательных частот определитель отрицателен и штриховка должна вестись справа при движении по кривой в сторону увеличения частот. Кривые, соответствующие положительным и отрицательным частотам, совпадают, следовательно, граница устойчивости будет иметь двойную штриховку.

Используем оставшиеся условия устойчивости:

и ,

что дает и , откуда получаем дополнительные границы области устойчивости и .

Построение области устойчивости в соответствии с полученными выражениями показано на рис. 93. Граница колебательного типа имеет двойную штриховку, поскольку её приходится при штриховке проходить дважды (для положительных частот и для отрицательных частот).

Дополнительные границы совпадают с осями координат и штрихуются "по смыслу". Колебательная граница имеет асимптоту, проходящую на уровне 1/T₁. Следует обратить внимание на то, что по горизонтальной оси графика откладывается параметр T₂ в соответствии с принятым построением определителя для правила штриховки.

Структурная устойчивость систем

Если неустойчивую систему можно привести в устойчивое состояние изменением ее параметров, то такая система называется структурно-устойчивой. Если никакое изменение параметров системы не приводит ее в устойчивое состояние, то такая система называется структурно-неустойчивой. Поскольку задача конструктора системы сводится к созданию работоспособной системы (т.е. устойчивой системы), то необходимы способы обеспечения устойчивости структурно-неустойчивых систем.

Рассмотрим пример системы, которая задана структурной схемой, приведенной на рис. 94. Система состоит из двух инерционных звеньев и одного интегрирующего звена. Все звенья соединены последовательно.

Исследуем устойчивость этой системы, используя, например, критерий Найквиста. Передаточная функция разомкнутой системы

, где - коэффициент усиления системы.

Частотную передаточную функцию определим по передаточной функции и представим в виде выражений для модуля и аргумента:

, .

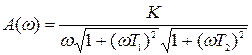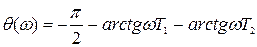АФЧХ системы обладает следующими особенностями: при , , а при , .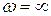

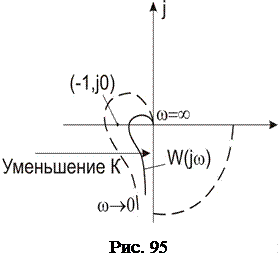График АФЧХ показан на рис. 95. Пунктиром показана частотная характеристика при большом коэффициенте усиления системы K. Замкнутая система в этом случае неустойчива, поскольку годограф W(jw) охватывает контрольную точку (-1,j0).

При уменьшении коэффициента усиления системы K годограф "стягивается" к началу координат и можно выбрать такое значение коэффициента усиления K, при котором замкнутая система становится устойчивой (годограф, показанный сплошной линией на рис. 95).

Следовательно, рассматриваемая система является структурно-устойчивой системой. Полуокружность, показанная пунктиром на рис. 95, необходима для условного замыкания АФЧХ астатической системы при использовании критерия устойчивости Найквиста.

Другой пример замкнутой системы показан структурной схемой на
рис. 96. Эта система состоит из инерционного звена и двух интегрирующих звеньев, включенных последовательно.

Передаточная функция системы

.

Соответственно модуль и аргумент частотной передаточной функции

, .

При , и при , .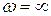

АФЧХ системы показана на рис. 97. Такая система будет неустойчивой при любых значениях K, поскольку контрольная точка
(-1,j0) всегда будет находиться внутри контура кривой. Не сможет изменить полученную картину и изменение постоянной времени T₁. Рассматриваемая система является структурно-неустойчивой, поскольку привести её к устойчивости изменением параметров системы невозможно.

Сделать структурно-неустойчивую систему устойчивой можно только путём изменения структуры системы. Приведение к устойчивости структурно-неустойчивой системы возможно двумя способами:

· введением дополнительных обратных связей, охватывающих неустойчивые звенья.

· введением дополнительных звеньев (стабилизирующих звеньев) в структуру системы.

Если в рассматриваемую систему ввести дополнительно реальное дифференцирующее звено с передаточной функцией

,

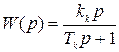то передаточная функция системы примет вид

.

Новая передаточная функция соответствует структурно-устойчивой системе, как это было видно из предыдущего примера. Дополнительно введённое реальное дифференцирующее звено выполнило функцию стабилизирующего звена.

Сложная система автоматического управления, имеющая в своем составе несколько простых замкнутых систем, является многоконтурной системой. Многоконтурная система будет структурно-устойчивой, если структурно-устойчивы все простые составляющие ее системы.

---

Дата добавления: 2015-09-02