Автоматического управления. Обыкновенная линейная система автоматического управления описывается

Обыкновенная линейная система автоматического управления описывается дифференциальным уравнением с постоянными коэффициентами

Для устойчивости системы необходимо, чтобы свободный процесс в ней был бы сходящимся. Свободные движения системыописываются левой частью исходного дифференциального уравнения и, следовательно, уравнение свободного процесса в системе

.

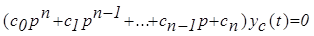Характеристическое уравнение замкнутой системы при этом запишется как

.

Характеристическое уравнение системы получается приравниванием к нулю знаменателя передаточной функции замкнутой системы.

Общее решение обыкновенного линейного дифференциального уравнения, имеющего порядок n:

,

где A_i – постоянные интегрирования, p_i – корни характеристического уравнения, n – число корней.

Корни характеристического уравнения могут быть как вещественными, так и комплексными (попарно сопряжёнными). Каждый комплексный корень порождает в решении уравнения слагаемое вида

,

где – начальная фаза, А_i – начальная амплитуда.

При решении характеристического уравнения системы возможны различные случаи, в зависимости от соотношения его коэффициентов (т.е. в зависимости от параметров системы).

1. Корни характеристического уравнения имеют отрицательные вещественные части. В этом случае для всех слагаемых

и, следовательно, свободный процесс затухает. Система устойчива, а графики переходного процесса показаны на рис. 76 (для каждого слагаемого).
На рис. 76а показан затухающий апериодический процесс, а на рис. 76б - затухающий колебательный процесс (пунктиром показана огибающая колебательного процесса). Апериодический процесс будет наблюдаться при чисто вещественном корне характеристического уравнения, колебательный – при комплексном корне.

2. Среди корней характеристического уравнения есть хотя бы один корень с положительной вещественной частью. В этом случае в общем решении дифференциального уравнения для свободного процесса появится слагаемое, стремящееся к бесконечности с увеличением времени:

и переходный процесс будет расходящимся (рис. 77). Графики показаны для одного слагаемого общего решения. Система в этом случае неустойчива.

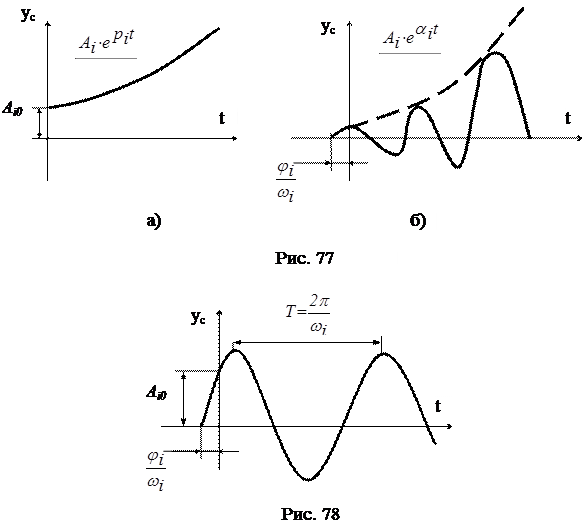
3. Характеристическое уравнение имеет хотя бы одну пару комплексных корней с нулевой вещественной частью. В решении дифференциального уравнения появляется гармоническая составляющая

,

порождающая незатухающую гармоническую составляющую переходного процесса (рис. 78). При переходный процесс системы будет носить характер незатухающих колебаний. Принято считать, что в этом случае система находится на границе устойчивости. Этот случай представляет чисто теоретический интерес и в реальных системах не наблюдается.

Рассмотренные случаи позволяют сформулировать математическое условие устойчивости для системы автоматического управления. Система автоматического управления будет устойчива, если все вещественные корни характеристического уравнения системы отрицательны, а все комплексные корни имеют отрицательные вещественные части.

Рис. 79

Если корни характеристического уравнения изобразить на комплексной плоскости, то для устойчивости системы необходимо, чтобы все они лежали бы в левой полуплоскости (рис. 79). На рис. 79 корни характеристического уравнения изображены кружками на комплексной плоскости. Границе устойчивости будет соответствовать нахождение хотя бы одной пары корней на мнимой оси (для них вещественная часть равна нулю).

Поскольку корни характеристического уравнения определяются величиной и знаком коэффициентов дифференциального уравнения, то изменение коэффициентов, вследствие изменения параметров системы, может привести к нарушению условия устойчивости. Для исследования устойчивости системы автоматического управления необходимо проверить выполнение условия устойчивости для дифференциального уравнения системы. Система, для которой условие устойчивости выполняется, будет устойчивой (т.е. работоспособной).

Дата добавления: 2015-09-02