Автоматического управления

Частотную передаточную функцию W(jw), являющуюся комплексным выражением, можно представить в векторной форме. При изменении частоты входного сигнала в пределах - < < + конец вектора опишет годограф, который называют амплитудно-фазовой частотной характеристикой (АФЧХ) (рис. 38).

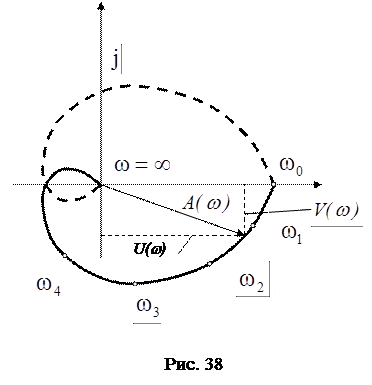АФЧХ строится по точкам. Отрицательная ветвь характеристики АФЧХ при (на рис. 38 показана пунктиром) зеркально отражает ветвь . Поэтому при анализе системы достаточно построить положительную ветвь АФЧХ при изменении частоты .

Амплитудно-фазовая частотная характеристика широко применяется при исследовании систем автоматического управления, например при исследовании устойчивости системы автоматического управления.

Наряду с АФЧХ частотные свойства системы описываются также логарифмическими частотными характеристиками (ЛХ): логарифмической амплитудно-частотной характеристикой (ЛАХ) и логарифмической фазовой частотной характеристикой (ЛФХ). Логарифмическая амплитудно-частотная характеристика обычно обозначается как L(w) и находится из соотношения дБ. Величина 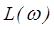выражается в децибелах.

Логарифмическая амплитудная частотная характеристика ЛАХ строится в координатах L(w) - w, при этом для оси w используется логарифмический масштаб. Использование логарифмического масштаба для оси частот приводит к тому, что эта ось разбивается на одинаковые участки – декады, в пределах которых частота увеличивается в 10 раз.

Логарифмическая фазовая характеристика ЛФХ строится в координатах . Координатные сетки обеих характеристик объединяются и представляются в общепринятой формуле, показанной на рис. 39.

Рис. 39

Особенностью построений на рис. 39 является то, что положительное направление оси θ(w) выбирается вниз – противоположно общепринятому направлению.

По оси абсцисс оцифровка ведется в единицах частоты , сами величины откладываются в логарифмическом масштабе. Частотный интервал, соответствующий удвоению частоты, называется октавой. Частотный интервал, соответствующий изменению частоты в 10 раз, называется декадой.

Достоинством логарифмических характеристик является их более простое построение, по сравнению с АФЧХ, а также возможность получения суммарной характеристики для соединения элементов простым суммированием ЛАХ и ЛФХ элементов.

Логарифмическая амплитудно-частотная характеристика строго может быть построена в том случае, когда передаточная функция не имеет размерности. Поэтому при построении логарифмических характеристик системы передаточную функцию системы следует преобразовать к такому виду, когда коэффициент преобразования системы становится безразмерным.

Дата добавления: 2015-09-02